Предмет: Геометрия,
автор: kolllb777
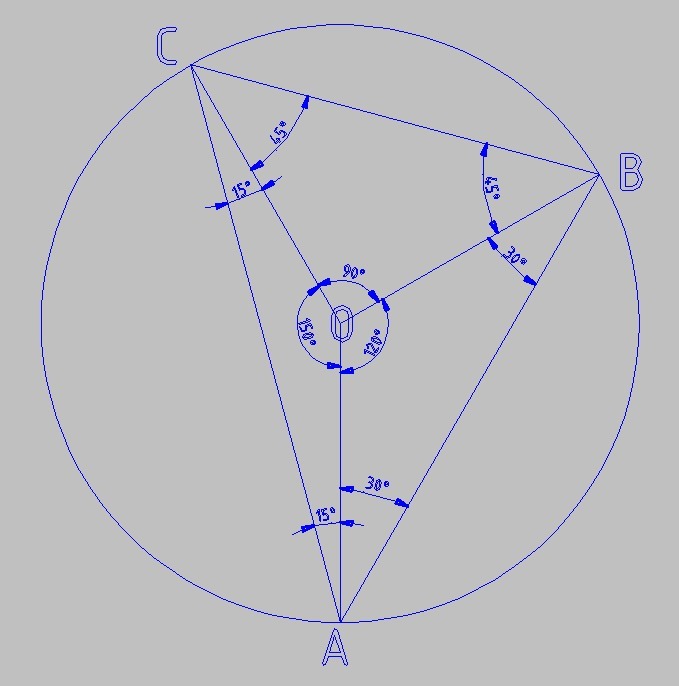
. Окружность с центром в точке О радиусом 16 см описана около треугольника ABCтак, что ∟OAB=300, ∟OCB=450. Найдите стороны AB и BCтреугольника
Ответы
Автор ответа:
2
Треугольники ОАВ и ОСВ равнобедренные - в каждом из них две стороны - это радиус окружности.
По условию даны углы при основании равнобедренных треугольников.
-------
ΔОАВ
∠ОАВ = 30°
∠ОВА = 30°
∠АОВ = 180 - 30*2 = 120°
По теореме косинусов
АВ² = 2*r² - 2*r²*cos(120°) = 3*r²
AB = r√3 = 16√3 см
-------------
ΔОCВ
∠ОCВ = 45°
∠ОВC = 45°
∠CОВ = 180 - 45*2 = 90°
По теореме Пифагора
СВ² = 2*r²
СB = r√2 = 16√2 см
По условию даны углы при основании равнобедренных треугольников.
-------
ΔОАВ
∠ОАВ = 30°
∠ОВА = 30°
∠АОВ = 180 - 30*2 = 120°
По теореме косинусов
АВ² = 2*r² - 2*r²*cos(120°) = 3*r²
AB = r√3 = 16√3 см
-------------
ΔОCВ
∠ОCВ = 45°
∠ОВC = 45°
∠CОВ = 180 - 45*2 = 90°
По теореме Пифагора
СВ² = 2*r²
СB = r√2 = 16√2 см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: ymnaya89
Предмет: Обществознание,
автор: sgorbunova240
Предмет: Русский язык,
автор: khlkaterin
Предмет: Математика,
автор: марюська228
Предмет: Литература,
автор: haur