Предмет: Математика,
автор: vovkatenvova
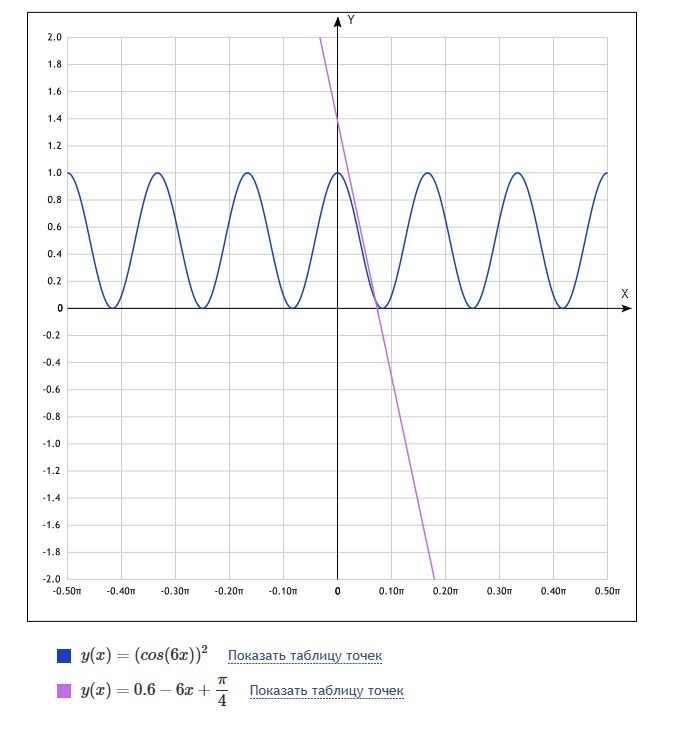
Напишите уравнение касательной к графику функции f (x)=cos^2 6x в точке x0=пи/24
Ответы
Автор ответа:
0
f(pi/24)=cos^2(6*pi/24)=cos^2(pi/4)=2/4=1/2
f`(x)=2cos(6x)*(-sin(6x))*6= -6sin(12x)
f`(pi/24)= -6sin(pi/20=-6
g(x)=f(pi/24)+f`(pi/24)(x-pi/24)=1/2-6(x-pi/24)=1/2-6x+pi/4-уравнение касательной
f`(x)=2cos(6x)*(-sin(6x))*6= -6sin(12x)
f`(pi/24)= -6sin(pi/20=-6
g(x)=f(pi/24)+f`(pi/24)(x-pi/24)=1/2-6(x-pi/24)=1/2-6x+pi/4-уравнение касательной
Приложения:
Похожие вопросы
Предмет: Математика,
автор: alnazif
Предмет: Математика,
автор: dilmiramaratova
Предмет: Русский язык,
автор: aleksejsy6050
Предмет: Алгебра,
автор: kshvidkaya
Предмет: География,
автор: baurzhan2