Предмет: Математика,
автор: soglnatali
Дана функция z=f(x;y). Показать, что она удовлетворяет данному уравнению.
Приложения:
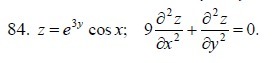
Ответы
Автор ответа:
3
Найдем первую и вторую частную производную по х (у-const).

Найдем первую и вторую частную производную по y (x-const).

Подставив в условие, получим

Что и требовалось показать )
Найдем первую и вторую частную производную по y (x-const).
Подставив в условие, получим
Что и требовалось показать )
Похожие вопросы
Предмет: Алгебра,
автор: nowikov4dash
Предмет: Алгебра,
автор: sonyyyyx
Предмет: Алгебра,
автор: adibirova
Предмет: Математика,
автор: asiaasas