Question

Средняя линия равнобедренного треугольника, параллельная основанию, делит данный треугольник на трапецию и треугольник с периметром 24 см. Основание данного треугольника равно 12 см. Доказать, что полученную трапецию можно вписать в окружность.

Answer 1

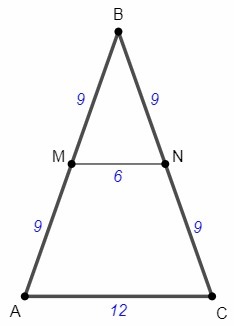
△ABC, AB=BC, AC=12
MN - средняя линия △ABC

MN=AC/2 =6
P(MBN)= MB+BN+MN <=> 2AB/2 +6 =24 <=> AB=18

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
AC+MN =12+6 =18
AM+NC =2AB/2 =18
В трапецию AMNC можно вписать окружность.