Предмет: Алгебра,
автор: alty4499
Помогииитеее (25 баллов)
Приложения:
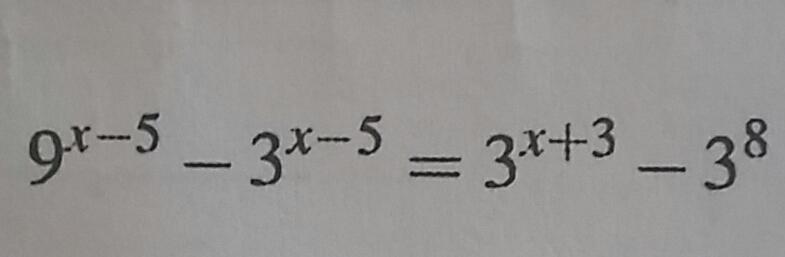
Ответы
Автор ответа:
1
Ответ: x1=5; x2=13
Похожие вопросы
Предмет: История,
автор: arturr636643
Предмет: Математика,
автор: bekramigra
Предмет: Математика,
автор: anastasiakornienko28
Предмет: Математика,
автор: MrCheese1
Предмет: Математика,
автор: vladdemesh24