Предмет: Алгебра,
автор: Natalyyy19
Решите неравенство(+- подробное решение)
Приложения:
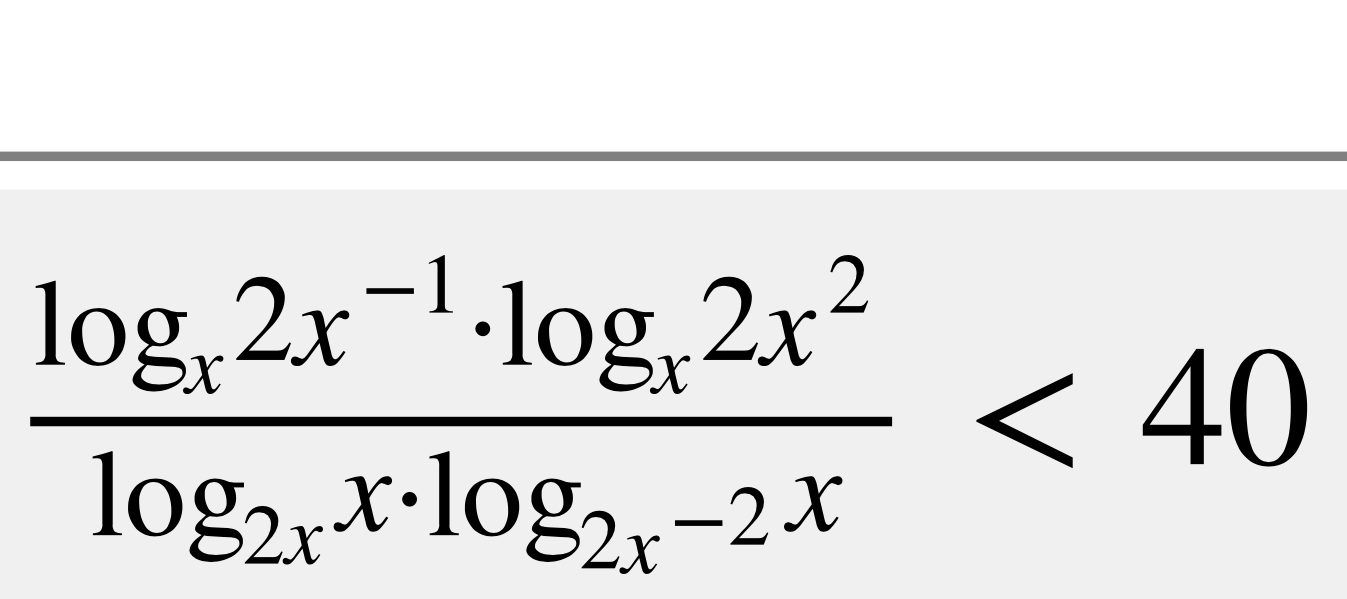
Ответы
Автор ответа:
0
x=/=1
x>0
Преобразовывая по формуле log(a)b=1/log(b)a
log(x)(2x^-1)*log(x)(2x^2)*log(x)(2x)*log(x)(2x^-2)<40
(log(x)2-1)(log(x)2+2)(log(x)2+1)(log(x)2-2)<40
log(x)2=t
(t^2-1)(t^2-4)<40
t^4-5t-36<0
D=13^2
t=9,-4
x E (0, 1/2^(1/3)) U (2^(1/3), +oo)
x>0
Преобразовывая по формуле log(a)b=1/log(b)a
log(x)(2x^-1)*log(x)(2x^2)*log(x)(2x)*log(x)(2x^-2)<40
(log(x)2-1)(log(x)2+2)(log(x)2+1)(log(x)2-2)<40
log(x)2=t
(t^2-1)(t^2-4)<40
t^4-5t-36<0
D=13^2
t=9,-4
x E (0, 1/2^(1/3)) U (2^(1/3), +oo)
Похожие вопросы
Предмет: Русский язык,
автор: bexruzibragimov
Предмет: Английский язык,
автор: gcfyff7ff6
Предмет: Математика,
автор: zaharogorodnik
Предмет: Математика,
автор: ZarinaKim
Предмет: Математика,
автор: AN11112003