Предмет: Математика,
автор: antha47
СРОЧНО! Помогите!?
Тригонометрическое уравнение, желательно подробнее.
Заранее спасибо
Приложения:
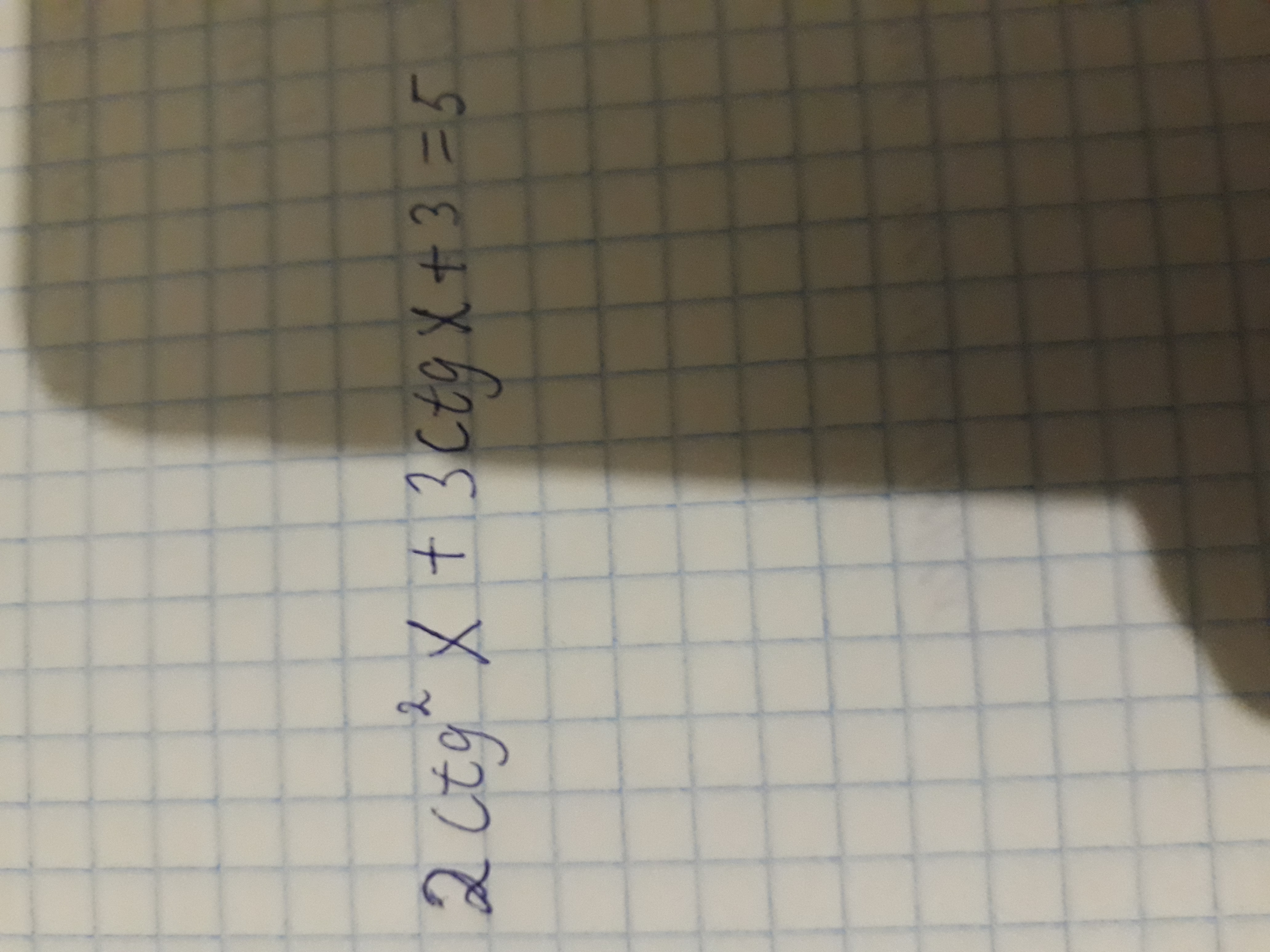
Ответы
Автор ответа:
1
1) 2ctg^2(x)+3ctg(x)+3=5
2ctg^2(x)+3ctg(x)-2=0
2) пусть ctg(x) = g ,тогда //делаем замену
2g^2+3g-2=0,
g1+g2=-(3/2); g1*g2=-1 (по т., об. т. Виета) p.s. или через дискриминант;
g1=1/2,
g2=-2.
3)ctg(x)=1/2; ctg(x)=-2; //возращаемся к исходной
По формуле общего вида триг-ого уравнения находим:
x = arcctg(1/2) + pi*n, где n принадлежит множеству целых чисел;
x = arcctg(-2) + pi*n, где n принадлежит множеству целых чисел;
По свойству arcctg избавляемся от отриц. в аргументе:
x = pi - arcctg (2) +pi*n, где n принадлежит множеству целых чисел;
//т.к. значения не табличные, то arcctg остается.
x = pi - arcctg (2) +pi*n, где n принадлежит множеству целых чисел,
x = arcctg(1/2) + pi*n, где n принадлежит множеству целых чисел.
Ответ:
x ∈ {π-arcctg2+πn, n∈Z; arcctg(1/2)+πn, n∈Z}
2ctg^2(x)+3ctg(x)-2=0
2) пусть ctg(x) = g ,тогда //делаем замену
2g^2+3g-2=0,
g1+g2=-(3/2); g1*g2=-1 (по т., об. т. Виета) p.s. или через дискриминант;
g1=1/2,
g2=-2.
3)ctg(x)=1/2; ctg(x)=-2; //возращаемся к исходной
По формуле общего вида триг-ого уравнения находим:
x = arcctg(1/2) + pi*n, где n принадлежит множеству целых чисел;
x = arcctg(-2) + pi*n, где n принадлежит множеству целых чисел;
По свойству arcctg избавляемся от отриц. в аргументе:
x = pi - arcctg (2) +pi*n, где n принадлежит множеству целых чисел;
//т.к. значения не табличные, то arcctg остается.
x = pi - arcctg (2) +pi*n, где n принадлежит множеству целых чисел,
x = arcctg(1/2) + pi*n, где n принадлежит множеству целых чисел.
Ответ:
x ∈ {π-arcctg2+πn, n∈Z; arcctg(1/2)+πn, n∈Z}
antha47:
А где pi это число пи?
да
Похожие вопросы
Предмет: Математика,
автор: dfvv14
Предмет: Математика,
автор: emaeangel1
Предмет: Биология,
автор: enelo444
Предмет: Математика,
автор: Ханна12342245
Предмет: Биология,
автор: диана870