Предмет: Математика,
автор: Kashena
Нужно решение интеграла способом замены переменной, срочно
Приложения:
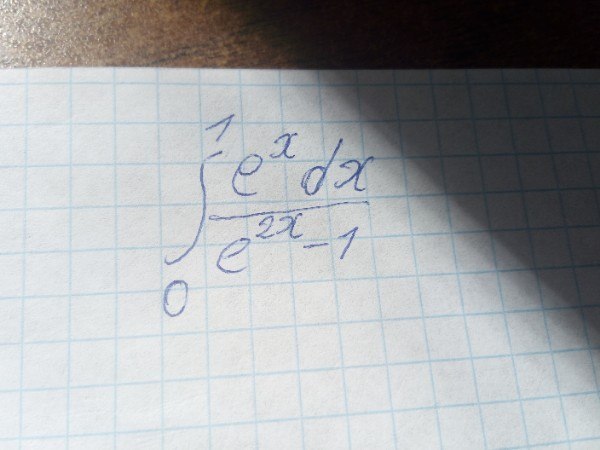
Ответы
Автор ответа:
1
Kashena:
почему у вас в решении вместо минуса в условии стоит плюс???
исправьте, пожалуйста
Похожие вопросы
Предмет: Физика,
автор: df973352danilka
Предмет: Геометрия,
автор: 23501amb
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: ЛизЦой
Предмет: Алгебра,
автор: MissKrash