Предмет: Геометрия,
автор: алгебра1998
. В некоторой трапеции длина одной из диагоналей равна сумме длин оснований трапеции, а угол между диагоналями равен 60 градусов. Доказать, что эта трапеция равнобокая
Ответы
Автор ответа:
0
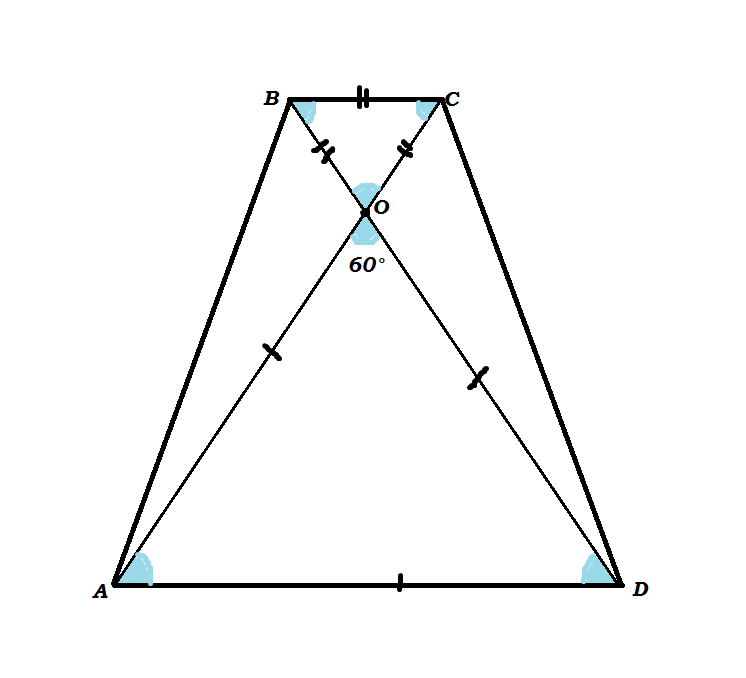
Пускай нам дана трапеция ABCD (ВС и АD - основания) ,
ее диагональ АС = ВС + AD
угол между диагоналями АС и ВD равен 60°
Доказать, что АВСD - равнобедренная трапеция
Доказательство:
проведем из пункта В прямую к диагонали АС (пункт пересечения обозначим О), так, что ВС = СО
тогда АО = АС - СО = (ВС + AD) - ВС = AD
имеем два равнобедренных треугольника ∆ВСО (ВС = СО) и ∆AOD (АО = AD)
<CBO = <COB (∆BCO- равнобедренный)
<AOD = <ADO (∆AOD- равнобедренный)
<BCO = <OAD (накрест лежащие) ==> <CBO = <COB = <AOD = <ADO
Раз <AOD = <BOC, а стороны АО и СО этих углов лежат на одной прямой, то <AOD и < BOC -вертикальные
и значит ВО и OD лежат на одной прямой ==>
O - пункт пересечения диагоналей AC и BD
тогда <BOC = AOD = 60° (по условию)
<CBO = <COB = <AOD = <ADO = 60°
<BCO = <OAD = 180 - <AOD - <ODA = 60° ==>
==> ∆BCO и ∆AOD - равносторонние
BC = CO = OB (∆BCO - равносторонний)
AO = OD = AD (∆AOD - равносторонний)
<BOA = <COD (вертикальные) ==>
==> ∆BOA = ∆COD (по двум сторонам и углу между ними)
значит BA = CD
и делаем вывод, что ABCD - равнобедренная трапеция
всё =)
ее диагональ АС = ВС + AD
угол между диагоналями АС и ВD равен 60°
Доказать, что АВСD - равнобедренная трапеция
Доказательство:
проведем из пункта В прямую к диагонали АС (пункт пересечения обозначим О), так, что ВС = СО
тогда АО = АС - СО = (ВС + AD) - ВС = AD
имеем два равнобедренных треугольника ∆ВСО (ВС = СО) и ∆AOD (АО = AD)
<CBO = <COB (∆BCO- равнобедренный)
<AOD = <ADO (∆AOD- равнобедренный)
<BCO = <OAD (накрест лежащие) ==> <CBO = <COB = <AOD = <ADO
Раз <AOD = <BOC, а стороны АО и СО этих углов лежат на одной прямой, то <AOD и < BOC -вертикальные
и значит ВО и OD лежат на одной прямой ==>
O - пункт пересечения диагоналей AC и BD
тогда <BOC = AOD = 60° (по условию)
<CBO = <COB = <AOD = <ADO = 60°
<BCO = <OAD = 180 - <AOD - <ODA = 60° ==>
==> ∆BCO и ∆AOD - равносторонние
BC = CO = OB (∆BCO - равносторонний)
AO = OD = AD (∆AOD - равносторонний)
<BOA = <COD (вертикальные) ==>
==> ∆BOA = ∆COD (по двум сторонам и углу между ними)
значит BA = CD
и делаем вывод, что ABCD - равнобедренная трапеция
всё =)
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: katapazejchuk
Предмет: География,
автор: volkovaalena86337
Предмет: Математика,
автор: Ayaulum153
Предмет: Математика,
автор: сгущ
Предмет: Химия,
автор: marishka1212