Предмет: Алгебра,
автор: ЯНеДаунЯГуманитарий
Найти значение выражения, если известно, что 

Ответы
Автор ответа:
2
Приложения:
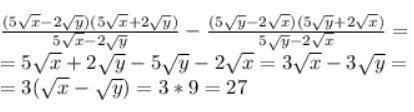
ЯНеДаунЯГуманитарий:
Спасибо, конечно, но система, по-моему, дала сбой)
фотку прикрепил, там решение
Все, работает, спасибо)
обнови страницу
Похожие вопросы
Предмет: География,
автор: DAFFI228
Предмет: Алгебра,
автор: avtostop
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: kazyuva30