Question

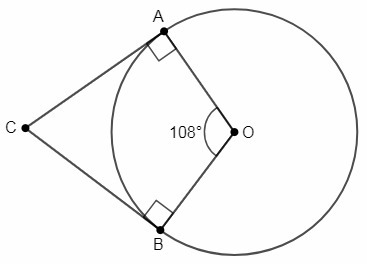
К окружности из точки с проведены касательные са и сб найдите градусную меру угла асб если градусная мера меньшей дуги аб равна 108 градусов

Answer 1

Сумма углов четырехугольника 360°. Касательная перпендикулярна радиусу, проведенному в точку касания, ∠A=∠B=90°. Центральный угол равен дуге, на которую опирается, ∠AOB=108°
∠С= 360°- 90°*2 -108° =72°

ИЛИ

Угол между касательными, проведенными из одной точки, равен полуразности большей и меньшей отсекаемых дуг. Отсекаемые дуги вместе составляют окружность, 360°.
∠C= ((360°-108°)-108°)/2 = 180°-108° =72°