Предмет: Математика,
автор: RutaS
Как найти корни данного уравнения? И количество корней
Приложения:
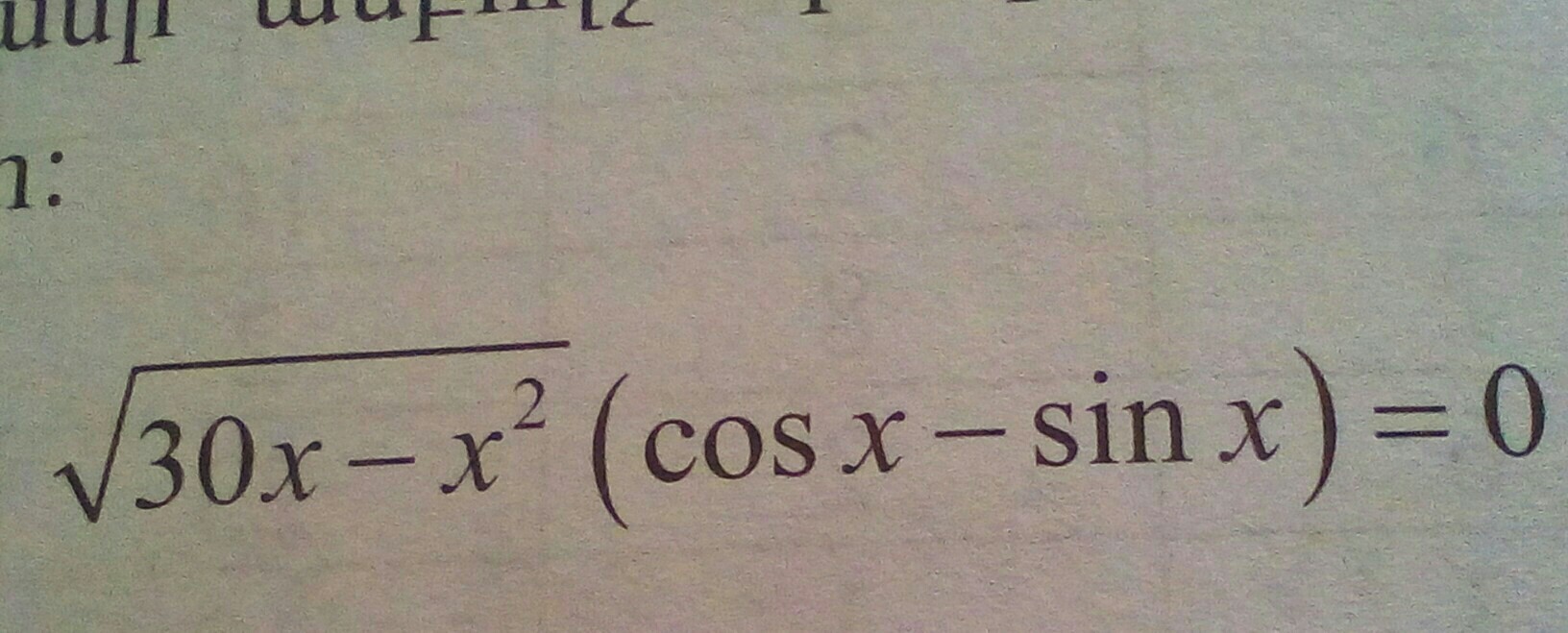
Ответы
Автор ответа:
1
Решаем каждое уравнение, составляем совокупность.
При этом, должно выполняться следующее ограничение:
Преобразуем:
Значит, решения:
RutaS:
Спасибо, большое за ответ. Если не сложно, пожалуйста, объясните, как вы получили последние корни
Сначала мы получили общее решение: pi/4 + pi*n, где n - целые
Затем из-за выражения под корнем поставили ограничение, что х находится в пределах от 0 до 30
Таким образом, мы выбрали такие n, чтобы x попадал в ОДЗ
Теперь лучше? :)
Спасибо огроомное
Обращайтесь :)
интересно что вы удалили мое решение, если оно идентично с этим, одз не проверяла, тк этот шаг делать бессмысленно, тк у нас все решения не выходят из одз!
Решения ой как выходят из одз. У вас решение тригонометрической части является периодическим. Значит, оно уходит в бесконечность как влево, так и вправо. При этом одз - [0;30]. Поэтому проверка одз имеет смысл.
Похожие вопросы
Предмет: Русский язык,
автор: fatimasafarova705
Предмет: История,
автор: alina90056jk
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Кира12121