Question

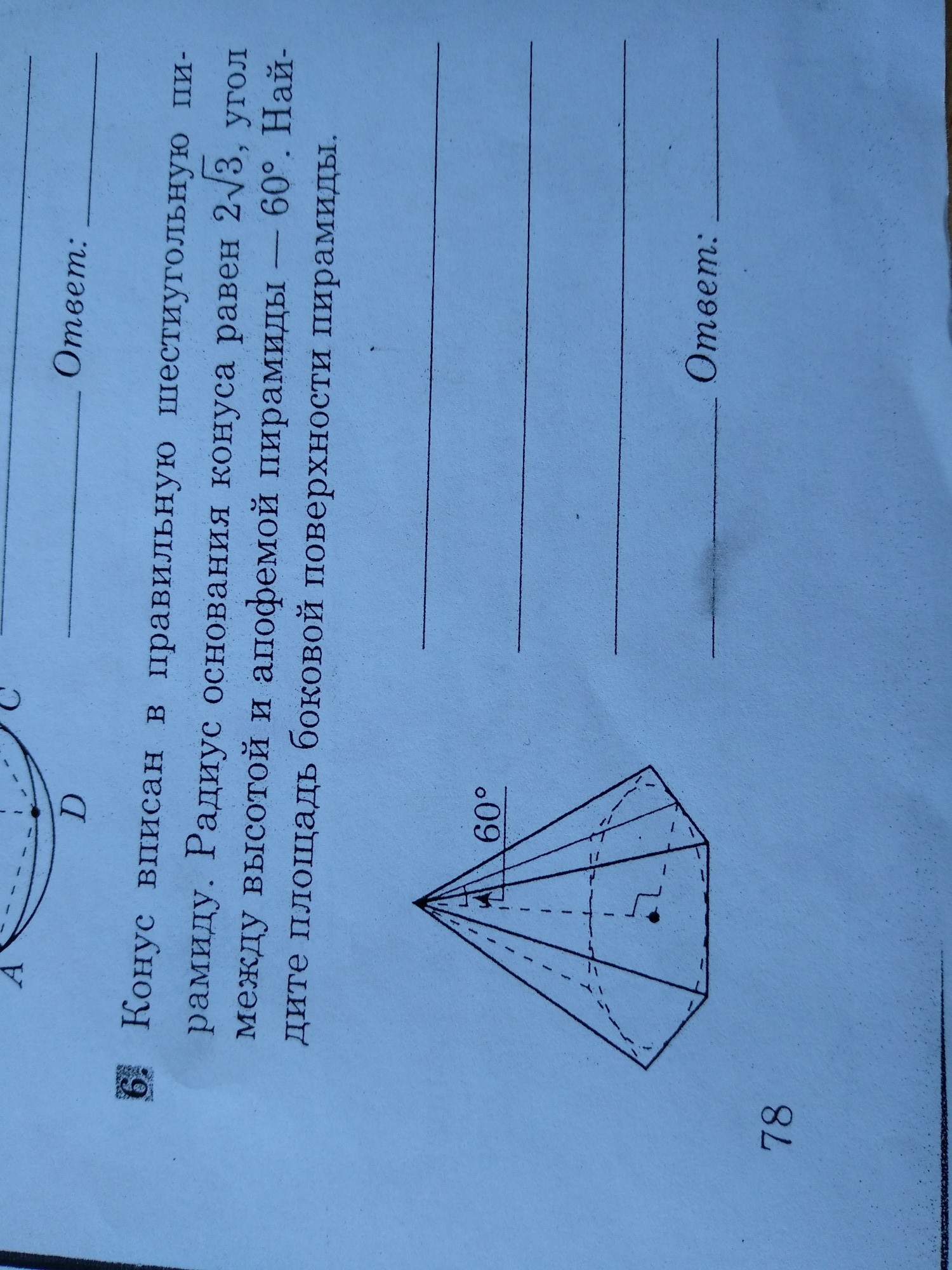
конус вписан в правильную шестиугольную пирамиду. радиус основания конуса равен
$2 \sqrt{3}$
угол между высотой и апофемой пирамиды - 60°. найдите площадь боковой поверхности пирамиды

Answer 1

По заданным значениям апофемы А = 18 см и углу наклона боковой грани α = 60 ° находим: - высота Н = А*sinα = 18*(√3/2) = 9√3 ≈ 15,588457 см, - радиус окружности. вписанной в основание r = A*cosα = 18*(1/2) = 9 см.Отсюда определяем сторону а основания, равную радиусу описанной окружности.а = r/(cos30°) = 9/(√3/2) = 18/√3 = 6√3 ≈ 10,392305 см.Периметр равен: Р = 6а = 6*(6√3) = 36√3 ≈ 62,353829 см.Теперь можно определить площадь Sбок боковой поверхности:Sбок = (1/2)РА = (1/2)*(36√3)*18 = 324√3 ≈ 561,18446 см².