Question

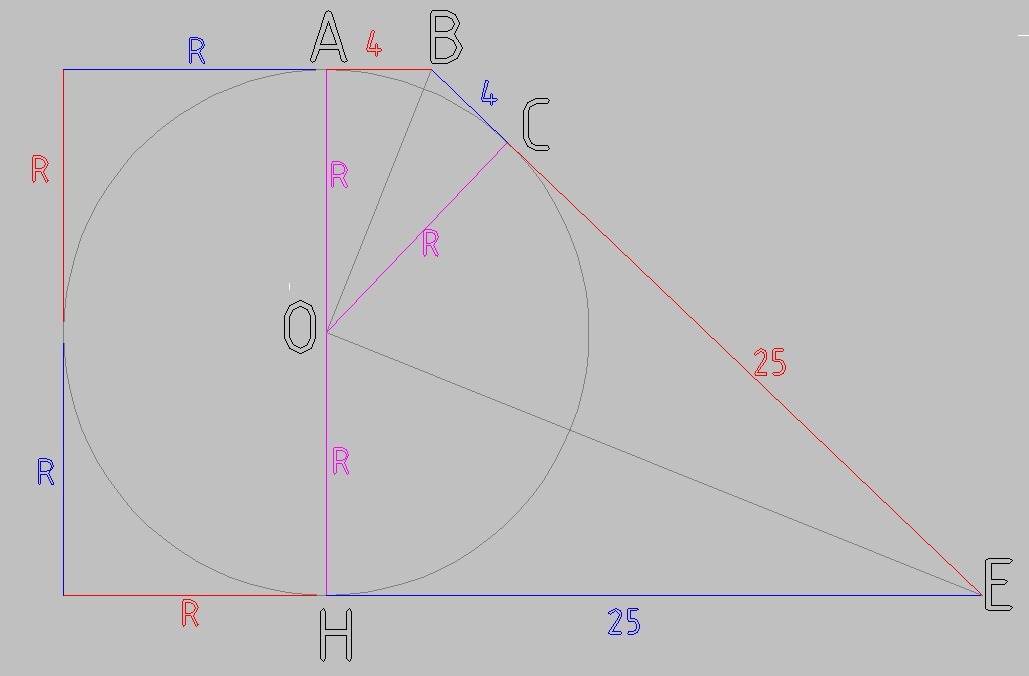
В прямоугольную трапецию вписана окружность.Точка касания делит большую из боковых сторон на отрезки 4 см и 25 см. Найти периметр трапеции.

Answer 1

пусть ∠НЕО = β
Тогда ∠СЕО = β
∠СЕН = 2β
∠АВС = 180 - 2β (как односторонние углы при параллельных основаниях трапеции и секущей)
∠СВО = ∠АВС/2 = 90 - β
∠ВОС = 90 - ∠СВО = 90 - (90 - β) = β
---
ΔВСО ~ ΔЕСО - один угол β, второй прямой
Из подобия
4/R = R/25
R² = 4*25 = 100
R = 10 см
Периметр
P = 4R + 2*(4+25) = 40 + 58 = 98 см