Question

Упростить: 1/(tg a + ctg a) * sin^2 a
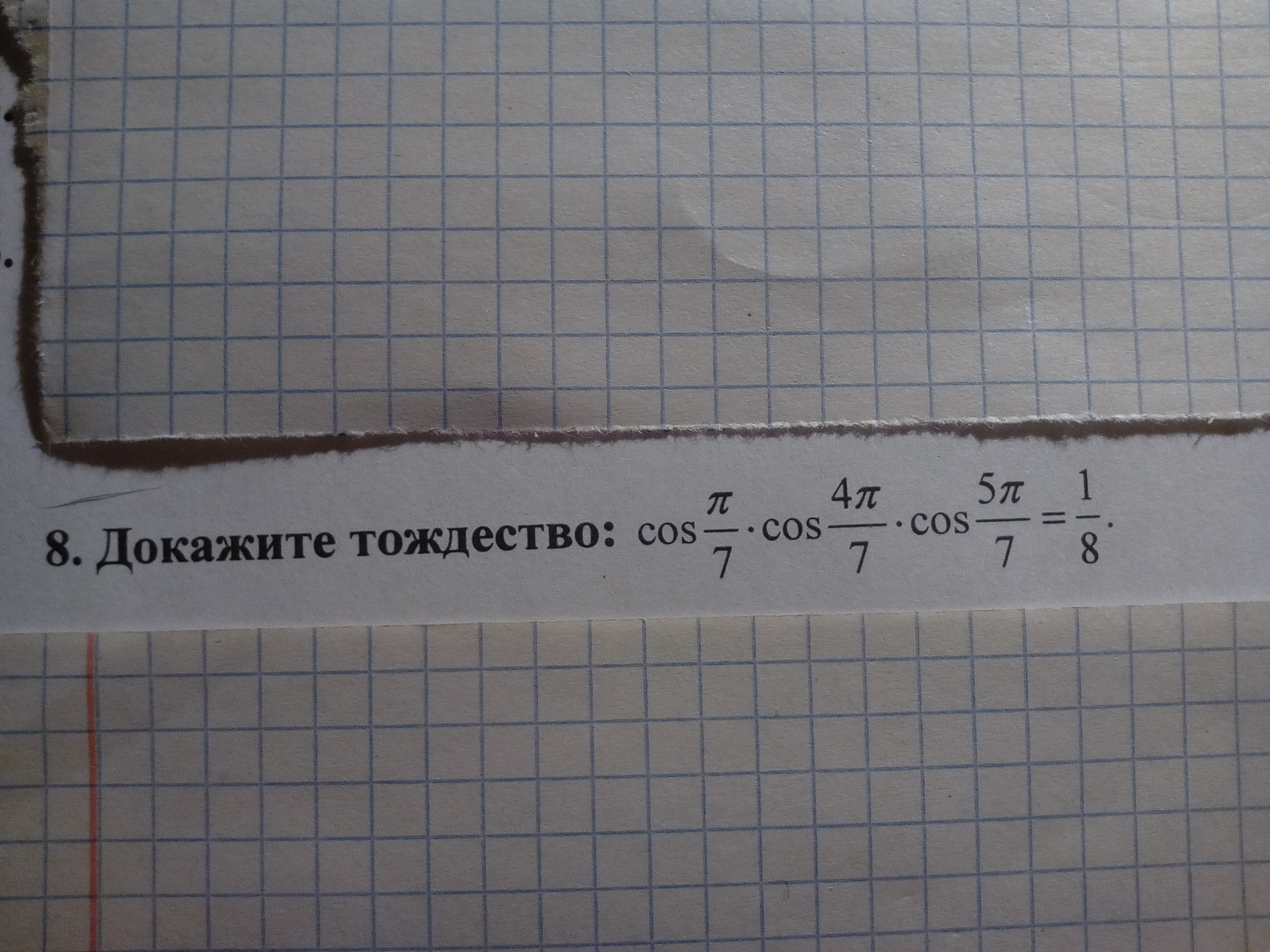
Доказать: cos п/7 * cos 4п/7 * 5п/7 = 1/8

Answer 1

1/((tga+ctga)*sin^2a) = 1/((sin^2a+cos^2a)*tga) = 1/tga  

 cos(pi/7)*cos(4pi/7)*cos(5pi/7) = 2*sin(pi/7)*cos(pi/7)*cos(4pi/7)*cos(5pi/7)/(2*sin(pi/7)) =  sin(2pi/7)*cos(4pi/7)*cos(5pi/7)/(2*sin(pi/7)) = 2*cos(2pi/7)*sin(2pi/7)*cos(4pi/7)*cos(5pi/7)/(4*sin(pi/7)*cos(2pi/7)) =  sin(4pi/7)*cos(4pi/7)*cos(5pi/7)/(4*sin(pi/7)*cos(2pi/7)) = sin(8pi/7)*cos(5pi/7)/(8*sin(pi/7)*cos(2pi/7)) = -sin(pi/7)*cos(pi-(2pi/7))/(8*sin(pi/7)*cos(2pi/7)) = 1/8