Question

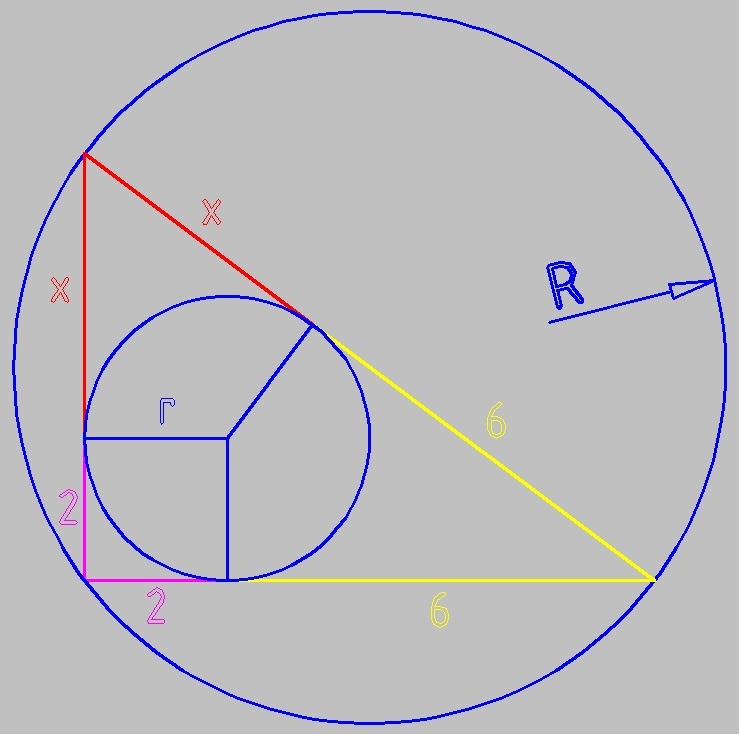
точка касания вписанной окружности делит катет прямоугольного треугольника на отрезки 2см и 6см считая от вершины прямого угла. найдите радиусы описанной и вписанной окружностей

Помогите с решением и рисунком
МНОГО БАЛЛОВ

Answer 1

Меньший из отрезков катета равен радиусу вписанной окружности
r = 2 см
меньший катет
a = 2+x см
больший катет
b = 2+6 = 8 см
гипотенуза
с = 6+x см
По теореме Пифагора
a² + b² = c²
(2+x) + 8² = (6+x)²
4 + 4x + x² + 64 = 36 + 12x + x²
68 = 36 + 8x
32 = 8x
x = 4 см
---
гипотенуза
с = 4+6 = 10 см
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
R = c/2 = 10/2 = 5 см