Предмет: Алгебра,
автор: mildgeneral
Помогите решить приведя основание логарифмов к 0,5. Никак не могу прийти к правильному ответу
Приложения:
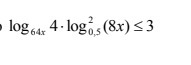
Ответы
Автор ответа:
0
Если преобразовать
![\\x\ \textgreater \ 0\\
log_{64x}4 = \frac{1}{log_{4}64x} = \frac{2}{log_{2}8+log_{2}(8x)}\\
log_{0.5}(8x) = - log_{2}(8x) \\
log_{2}(8x)=t\\
\frac{2log^2_{2}(8x)}{3+log_{2}(8x}} \leq 3 \\
\frac{2t^2}{3+t} \leq 3 \\
t \neq -3\\
2t^2 \leq 9+3t \\
2t^2-3t-9 \leq 0 \\
(2t+3)(t-3) \leq 0 \\
t \in [ -\frac{3}{2}; 3] \cup (-\infty ; -3) \\
\\
-\frac{3}{2} \leq log_{2}(8x) \leq 3 \\
2^{-\frac{9}{2}} \leq x \leq 1 \\
\\
log_{2}(8x)\ \textless \ -3 \\
x \ \textless \ \frac{1}{64}\\
x\ \textgreater \ 0 \\\\
\\x\ \textgreater \ 0\\
log_{64x}4 = \frac{1}{log_{4}64x} = \frac{2}{log_{2}8+log_{2}(8x)}\\
log_{0.5}(8x) = - log_{2}(8x) \\
log_{2}(8x)=t\\
\frac{2log^2_{2}(8x)}{3+log_{2}(8x}} \leq 3 \\
\frac{2t^2}{3+t} \leq 3 \\
t \neq -3\\
2t^2 \leq 9+3t \\
2t^2-3t-9 \leq 0 \\
(2t+3)(t-3) \leq 0 \\
t \in [ -\frac{3}{2}; 3] \cup (-\infty ; -3) \\
\\
-\frac{3}{2} \leq log_{2}(8x) \leq 3 \\
2^{-\frac{9}{2}} \leq x \leq 1 \\
\\
log_{2}(8x)\ \textless \ -3 \\
x \ \textless \ \frac{1}{64}\\
x\ \textgreater \ 0 \\\\](https://tex.z-dn.net/?f=%5C%5Cx%5C+%5Ctextgreater+%5C+0%5C%5C+%0Alog_%7B64x%7D4+%3D+%5Cfrac%7B1%7D%7Blog_%7B4%7D64x%7D+%3D+%5Cfrac%7B2%7D%7Blog_%7B2%7D8%2Blog_%7B2%7D%288x%29%7D%5C%5C%0Alog_%7B0.5%7D%288x%29+%3D++-+log_%7B2%7D%288x%29+%5C%5C%0Alog_%7B2%7D%288x%29%3Dt%5C%5C+%0A%5Cfrac%7B2log%5E2_%7B2%7D%288x%29%7D%7B3%2Blog_%7B2%7D%288x%7D%7D+++%5Cleq++3+++%5C%5C+%0A+%5Cfrac%7B2t%5E2%7D%7B3%2Bt%7D+%5Cleq++3+%5C%5C+%0A+++++t+%5Cneq+-3%5C%5C%0A++2t%5E2++%5Cleq++9%2B3t+%5C%5C+%0A+2t%5E2-3t-9++%5Cleq++0+%5C%5C++++%0A++%282t%2B3%29%28t-3%29++%5Cleq++0+%5C%5C+%0A+t+%5Cin+%5B+-%5Cfrac%7B3%7D%7B2%7D%3B+3%5D+%5Ccup+%28-%5Cinfty+%3B+-3%29+%5C%5C%0A%5C%5C%0A+-%5Cfrac%7B3%7D%7B2%7D++%5Cleq++log_%7B2%7D%288x%29++%5Cleq++3+%5C%5C+%0A+2%5E%7B-%5Cfrac%7B9%7D%7B2%7D%7D++%5Cleq++x++%5Cleq++1+%5C%5C%0A%5C%5C%0A++log_%7B2%7D%288x%29%5C+%5Ctextless+%5C+-3+%5C%5C+%0A++x+%5C+%5Ctextless+%5C++%5Cfrac%7B1%7D%7B64%7D%5C%5C%0A+x%5C+%5Ctextgreater+%5C+0+%5C%5C%5C%5C%0A+++++%0A)
![2^{-\frac{9}{2}} \leq x \leq 1 \\
\\
x \in (0 , \frac{1}{64} ) \cup [\frac{1}{\sqrt{512}}, 1] 2^{-\frac{9}{2}} \leq x \leq 1 \\
\\
x \in (0 , \frac{1}{64} ) \cup [\frac{1}{\sqrt{512}}, 1]](https://tex.z-dn.net/?f=2%5E%7B-%5Cfrac%7B9%7D%7B2%7D%7D++%5Cleq++x++%5Cleq++1+%5C%5C+%0A++%5C%5C+%0A+x+%5Cin+%280+%2C+%5Cfrac%7B1%7D%7B64%7D+%29+%5Ccup++%5B%5Cfrac%7B1%7D%7B%5Csqrt%7B512%7D%7D%2C+1%5D)
mildgeneral:
z g
я прекрасно понимаю, как решать это неравенство через основание 2, просто принципиально хочу решить его через 0,5 и не получаю нужного ответа
Автор ответа:
0
А зачем тебе такое основание? Лучше сделать основание = 2.
пробуем?
1) log₆₄ₓ4 = log₂4/log₂(64x) = 2/(log₂64 +log₂x) = 2/(6 +log₂x);
2) log₀₎₅²(8x) = log₀₎₅(8x) * log₀₎₅(8x) = log₂(8x)/log₂0,5 * log₂(8x)/log₂0,5 =
=(log₂8 + log₂x)/(-1) * (log₂8 + log₂x)/(-1) =
=(3 +log₂x)(3 +log₂x)= 9 +6log₂x + log₂²x.
3) теперь наш пример: 2/(6 +log₂x) * (9 +6log₂x + log₂²x) ≤ 3 , ⇒
⇒ 2(9 +6log₂x + log₂²x)/(6 +log₂x) -3 ≤ 0, ⇒
⇒(18 +12log₂x + 2log₂²x -18 -3log₂x)/(6 +log₂x) ≤ 0,⇒
⇒(2log₂²x + 9log₂x)/(6 +log₂x) ≤ 0
метод интервалов.
ищем нули числителя. Это 0 и - 4,5
для знаменателя это - 6
-∞ - 6 -4,5 0 +∞
+ + - + это знаки (2log₂²x + 9log₂x)
- + + + это знаки (6 +log₂x)
IIIIIIIIIIIIIII IIIIIIIIIIIIIIII
a) log₂x < -6 x ≤1/64
x > 0, ⇒ x > 0 вывод: х∈(0;1/64)
б) -4,5 ≤ log₂x ≤ 0 , ⇒1/512 ≤ x ≤ 1
пробуем?
1) log₆₄ₓ4 = log₂4/log₂(64x) = 2/(log₂64 +log₂x) = 2/(6 +log₂x);
2) log₀₎₅²(8x) = log₀₎₅(8x) * log₀₎₅(8x) = log₂(8x)/log₂0,5 * log₂(8x)/log₂0,5 =
=(log₂8 + log₂x)/(-1) * (log₂8 + log₂x)/(-1) =
=(3 +log₂x)(3 +log₂x)= 9 +6log₂x + log₂²x.
3) теперь наш пример: 2/(6 +log₂x) * (9 +6log₂x + log₂²x) ≤ 3 , ⇒
⇒ 2(9 +6log₂x + log₂²x)/(6 +log₂x) -3 ≤ 0, ⇒
⇒(18 +12log₂x + 2log₂²x -18 -3log₂x)/(6 +log₂x) ≤ 0,⇒
⇒(2log₂²x + 9log₂x)/(6 +log₂x) ≤ 0
метод интервалов.
ищем нули числителя. Это 0 и - 4,5
для знаменателя это - 6
-∞ - 6 -4,5 0 +∞
+ + - + это знаки (2log₂²x + 9log₂x)
- + + + это знаки (6 +log₂x)
IIIIIIIIIIIIIII IIIIIIIIIIIIIIII
a) log₂x < -6 x ≤1/64
x > 0, ⇒ x > 0 вывод: х∈(0;1/64)
б) -4,5 ≤ log₂x ≤ 0 , ⇒1/512 ≤ x ≤ 1
Похожие вопросы
Предмет: Алгебра,
автор: Oaoamo
Предмет: Английский язык,
автор: vlad224423
Предмет: Русский язык,
автор: aishat203050
Предмет: Алгебра,
автор: yoyuyi