Предмет: Алгебра,
автор: jeandri
Решите уравнение
_______________
Приложения:
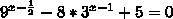
Ответы
Автор ответа:
1
Пусть
Ответ:
jeandri:
немного не понимаю момент после ввода переменной
заменил 3^x на t
затем домножил на 3
а там уж квадратное уравнение
аа, на 3, все, сглупила
Большое спасибо
Похожие вопросы
Предмет: Английский язык,
автор: mrmatrix101012
Предмет: Геометрия,
автор: snakeprofile879
Предмет: Музыка,
автор: komradgrigoriev2011
Предмет: Экономика,
автор: moiseenkonasta
Предмет: Алгебра,
автор: дима1068