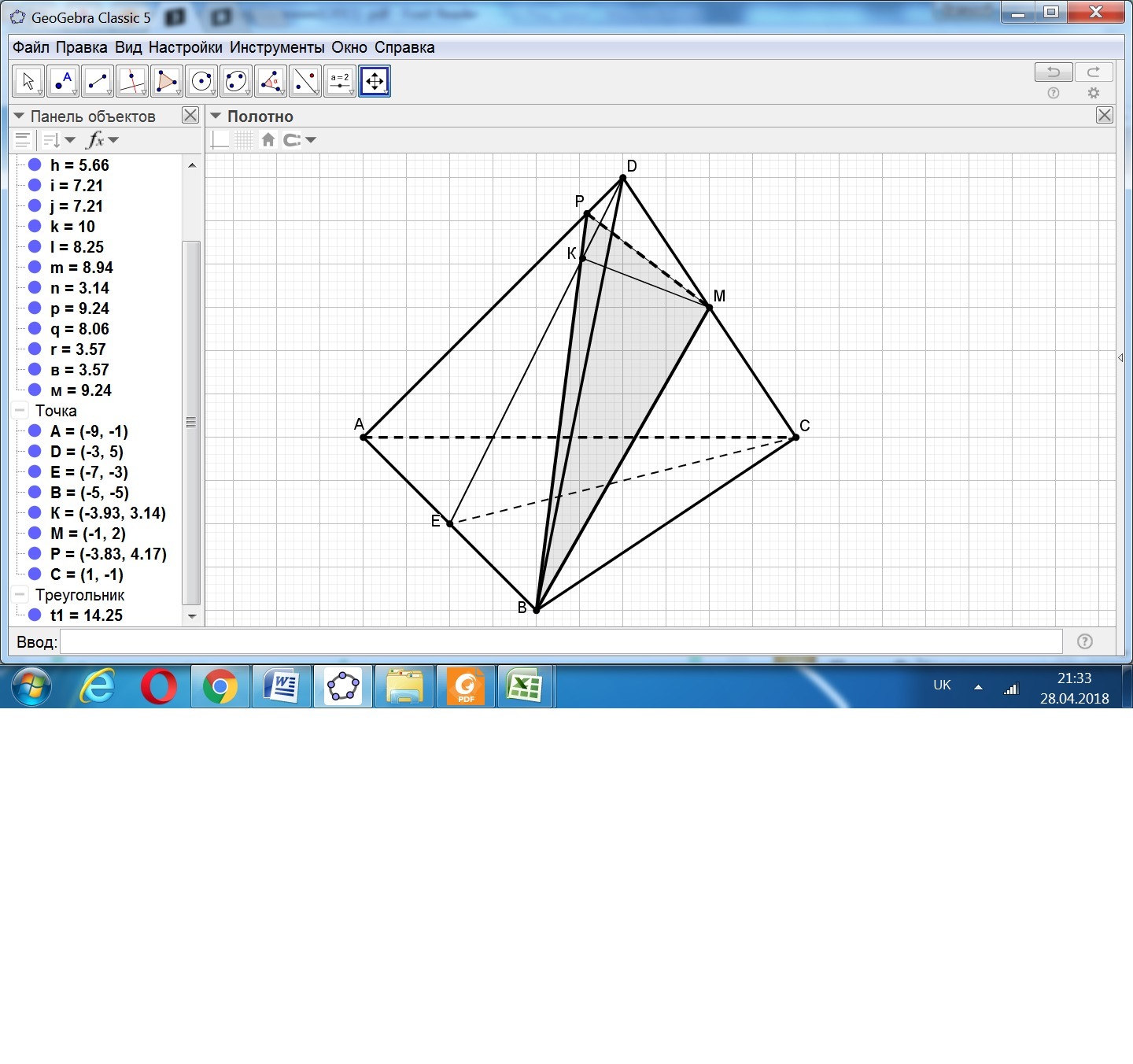
В правильном тетраэдре ABCD точка М – середина ребра CD. Построить сечение тетраэдра плоскостью, проходящей через прямую ВМ и перпендикулярной плоскости ABD. Найти площадь сечения, если |AB| = a.
Ответы
В правильном тетраэдре ABCD все рёбра равны между собой, а грани - правильные
треугольники.
Примем для удобства длину ребра а = 1.
В грани ABD проведём апофему DЕ.
Плоскость CDЕ перпендикулярна
плоскости ABD.
Из точки М опустим перпендикуляр МК на DЕ.
След заданной секущей плоскости в грани ABD будет
проходить через отрезок ВК - обозначим его ВР.
Получим в сечении треугольник МВР.
Сторона ВМ как медиана и
высота равна √3/2.
Рассмотрим плоскость CDЕ. Надо
определить положение точки К.
Проведём среднюю линию ММ1, она равна половине высоты основания СЕ, то есть (√3/2)/2 = √3/4.
Высота DО как высота правильного тетраэдра
равна √(2/3).
Проекция ОЕ апофемы DЕ на основание -
это (1/3) высоты основания СЕ. То есть ОЕ = (1/3)*(√3/2) = √3/6.
Тангенс угла DЕО равен √(2/3)/(√3/6) =
2√2.
Косинус этого угла равен 1/√(1+(2√2)²) = 1/3.
Отрезок КМ1 = ММ1*cos DЕО = (√3/4)*(1/3)
= √3/12.
Тогда ЕК = (√3/4) + (√3/12) = 4√3/12
= √3/3.
Рассмотрим грань АВD.
Тангенс угла РВА равен тангенсу угла КВЕ =
(√3/3)/(1/2) = 2√3/3.
Определим проекцию АР1 точки Р на АВ.
Примем её за х.
x*tg 60° = (1-x)*tg (KBE).
x*√3 = 2√3/3 - (2√3/3)*x.
Отсюда х = 2/5.
В плоскости АВD размер по высоте равен х*tg
60° = 2√3/5.
Тогда длина отрезка AР = √((2/5)² + (2√3/5)²)
= √((4/25) + (12/25)) = 4/5.
Отрезок РD давен 1 – (4/5) = 1/5,
Отрезок ВР = √((1-(2/5))² + (2√3/5)²) = √((9/25) +
(12/25)) = √21/5.
Осталось найти длину отрезка РМ.
Её найдём по теореме косинусов: РМ = √((1/5)2+(1/2)2-2*(1/5)*(1/2)*cos60) = √19/10.
Теперь находим площадь заданного сечения - треугольника ВРМ – которая определяется по формуле:
S(ВРМ) = √(p(p-a)(p-b)(p-c)).
Подставляем длины сторон: ВР = √21/5, РМ = √19/10 и ВМ = √3/2.
Полупериметр р = (a+b+c)/2 = 1,109215.
Подставив значения в формулу, получим S = 0,187083.
С учётом задания, что сторона равна а, то окончательный ответ:
S = 0,187083 а².