Предмет: Алгебра,
автор: Rafaelnodat1
как решать эти примеры? (интегралы) все на фото 18 и 19 задания
Приложения:
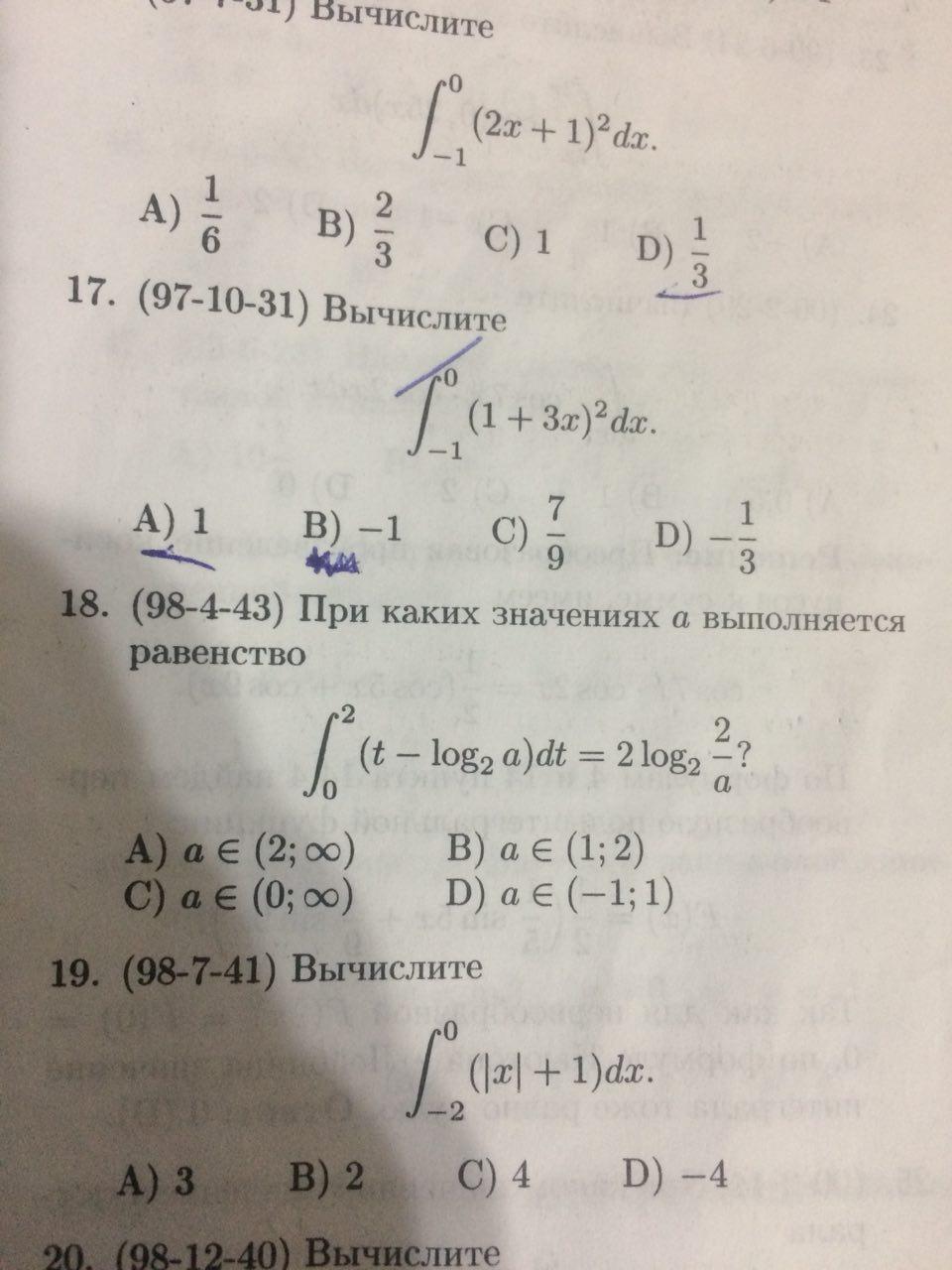
Ответы
Автор ответа:
1
18. ОДЗ по логарифму а>0
Вначале вычислить интеграл
 t²/2 - t*log₂a |²₀ =
t²/2 - t*log₂a |²₀ =
= (4/2 - 2log₂a) - (0 - 0) = 2 - 2log₂a = 2(1 - log₂a) =
= 2 (log₂2 - log₂a) = 2 log₂(2/a) ⇒
 ⇔
⇔ 
Полученное равенство справедливо для всех a>0 ⇒
Ответ C) a∈(0; +∞)
19. Так как функция f(x)=|x|+1 симметрична относительно прямой x=0 ⇒
 ⇔
⇔ 
 x²/2 + x |²₀ = 2²/2 + 2 - 0 = 4
x²/2 + x |²₀ = 2²/2 + 2 - 0 = 4
Ответ С) 4
Если решать без симметрии. Интервал интегрирования x∈[-2;0] ⇒
-2 ≤ x ≤ 0 ⇒ |x| = -x

= x - x²/2 |⁰₋₂ = 0 - 0 - (-2 - (-2)²/2) = -(-4) = 4
Ответ С) 4
Вначале вычислить интеграл
= (4/2 - 2log₂a) - (0 - 0) = 2 - 2log₂a = 2(1 - log₂a) =
= 2 (log₂2 - log₂a) = 2 log₂(2/a) ⇒
Полученное равенство справедливо для всех a>0 ⇒
Ответ C) a∈(0; +∞)
19. Так как функция f(x)=|x|+1 симметрична относительно прямой x=0 ⇒
Ответ С) 4
Если решать без симметрии. Интервал интегрирования x∈[-2;0] ⇒
-2 ≤ x ≤ 0 ⇒ |x| = -x
= x - x²/2 |⁰₋₂ = 0 - 0 - (-2 - (-2)²/2) = -(-4) = 4
Ответ С) 4
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: sashaays19
Предмет: Геометрия,
автор: anton173665
Предмет: Геометрия,
автор: Alex364