Помогите! Очень нужно с рисунком!
Через точку M, лежащую между параллельными плоскостями альфа и бета, проведены прямые a и b. Прямая a пересекает плоскости альфа и бета в точках A1 и A2, соответственно, прямая b - в точках B1 и B2. Найдите отрезок MB2, если A1 B2:A2 B2=3:4, B1B2=14 см.
Ответы
Ответ:
МВ2 = 8см
Объяснение:
Поправим описку в условии. Будем считать, что A1B1 : A2B2 = 3 : 4.
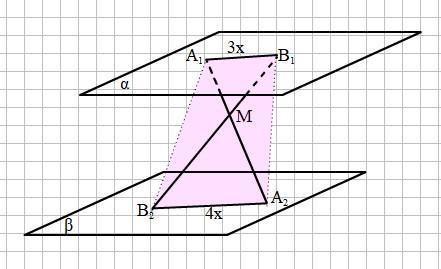
Смотри рисунок на прикреплённом фото.
Пусть А1В1 = 3х, тогда А2В2 = 4х.
Пересекающиеся прямые а и b образуют плоскость А1В1В2А2, которая пересекает параллельные плоскости α и β. Линии пересечения - это А1В1 и А2В2. Известно, что если некоторая плоскость пересекает параллельные плоскости, то линии пересечения параллельны, то есть А1В1║А2В2.
ΔА1В1М ~(подобен) ΔА2В2М по двум равным углам (∠В1А1М = В2А2М как накрест лежащие при А1В1║А2В2 и секущей А1А2; ∠А1В1М = ∠А2В2М как накрест лежащие при А1В1║А2В2 и секущей В1В2).
Соответствующие стороны Δ А1В1М и Δ А2В2М пропорциональны, поэтому А1В1 : А2В2 = МВ1 : МВ2 или
3х : 4х = (14 - МВ2) : МВ2
3 МВ2 = 4 · 14 - 4 МВ2
7 МВ2 = 56
МВ2 = 8(см)