Предмет: Математика,
автор: xXColdXx
Помогите найти производную высших порядков! Y с 4 штрихами, Z.
Смотрите на снимке. Буду признателен за помощь. Заранее спасибо.
Приложения:
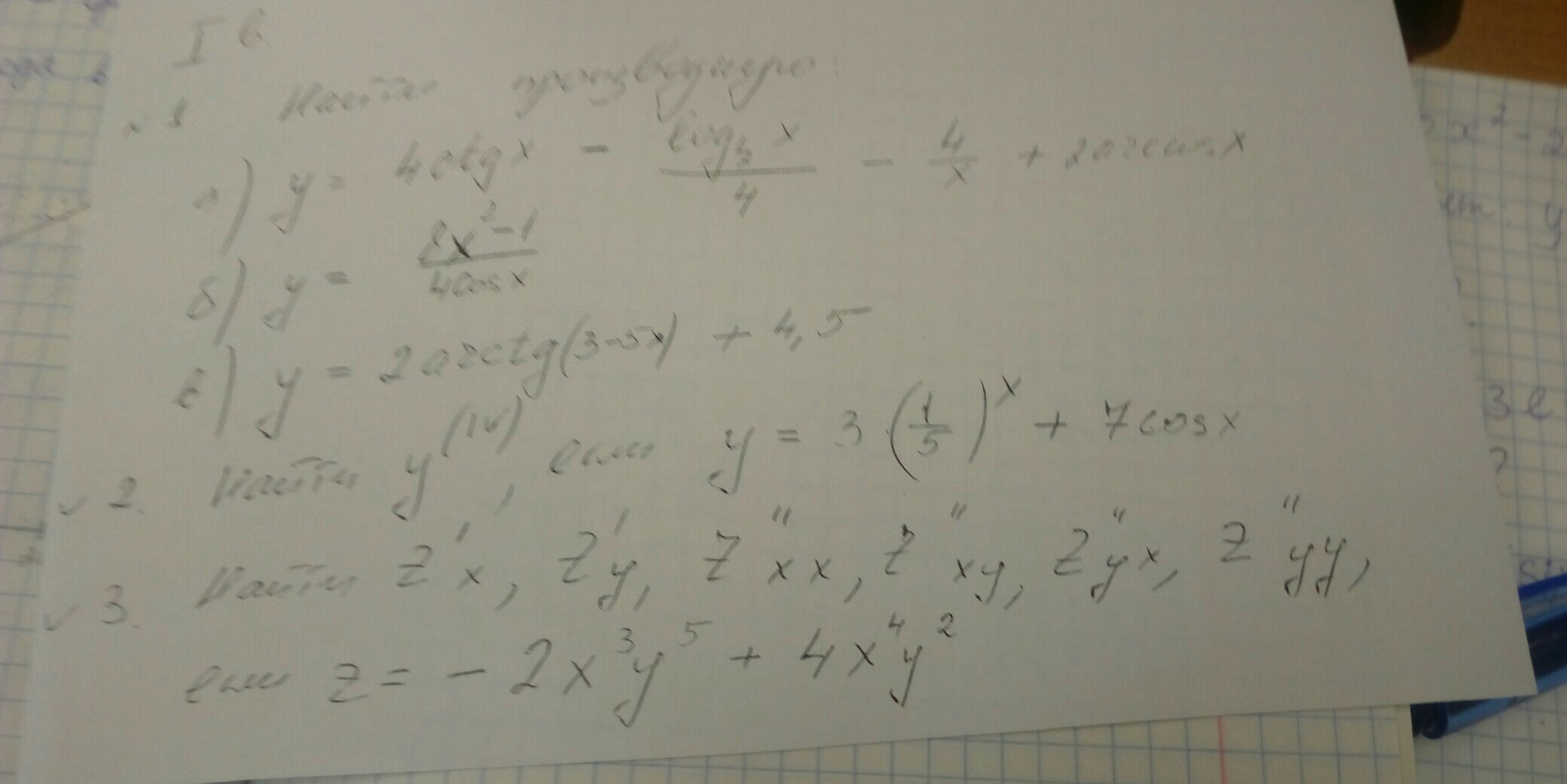
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: xomjk2910
Предмет: Українська мова,
автор: oksankavidis
Предмет: Алгебра,
автор: sofyamyau
Предмет: Математика,
автор: korobeinikoff