Предмет: Алгебра,
автор: PixelMan
Помогите с неравенством (не подробно)
Приложения:
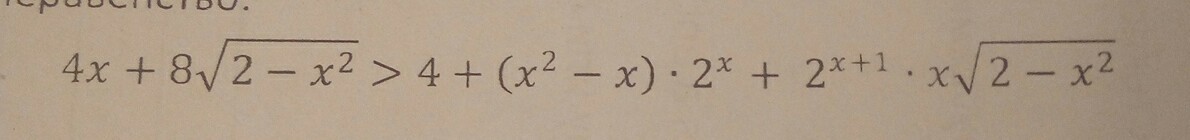
Ответы
Автор ответа:
2
Предложу такое решение:


Найдем нули множителей

Второй корень посторонний x<1
теперь второй множитель

заметим, что при х<0 второй множитель будет положительным для любых х
при х>0
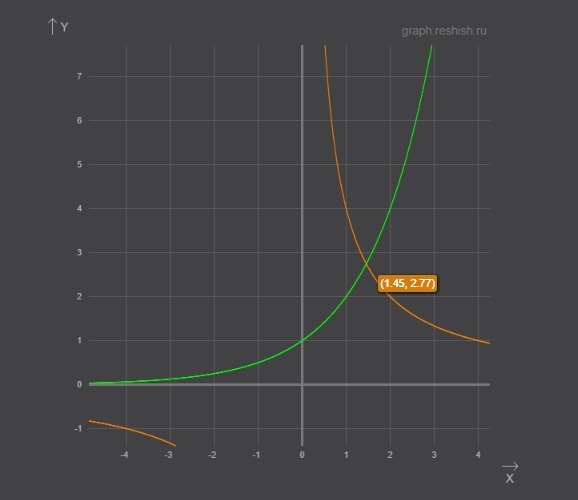
решим графически

Графики в приложении
по графику видим что корень есть и лежит вне области ОДЗ
проверим
х=√2

Значит на ОДЗ Второй множитель положителен
На знак неравенства влияет только точка перехода х=-1
___ - √2 ____ - 1 ______√2 ____
- +
Ответ : (-1; √2]
Найдем нули множителей
Второй корень посторонний x<1
теперь второй множитель
заметим, что при х<0 второй множитель будет положительным для любых х
при х>0
решим графически
Графики в приложении
по графику видим что корень есть и лежит вне области ОДЗ
проверим
х=√2
Значит на ОДЗ Второй множитель положителен
На знак неравенства влияет только точка перехода х=-1
___ - √2 ____ - 1 ______√2 ____
- +
Ответ : (-1; √2]
Приложения:
Похожие вопросы