Предмет: Математика,
автор: seregarulitru
Помогите вычислить определенный интеграл
Приложения:
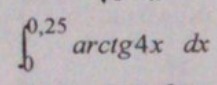
Ответы
Автор ответа:
1
seregarulitru:
Я также решал, мне учитель сказал, что при замене надо менять границы интегрирования
тут не замена. Тут интегрирование по частям, никаких замен границ не надо
А.... я кажется понял про какую замену речь идет. Я вместо замены сделал подведение под дифференциал.
Дополнил ответ
Похожие вопросы
Предмет: Литература,
автор: pechenca2000
Предмет: Другие предметы,
автор: ttalipov965
Предмет: История,
автор: uryvskaasofa
Предмет: Алгебра,
автор: tanuk87
Предмет: Математика,
автор: котик610