Предмет: Математика,
автор: alina44511
Найти: а) частное решение линейного однородного дифференциального уравнения второго подряда с постоянными коэффициентами,удовлетворяющее заданным начальным условиям. б) общее решение линейного наоднородного диффер. уравнения второго порядка с постоянными коэффициентами. Помогите пожалуйста!!
Приложения:
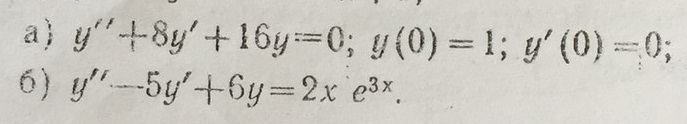
Ответы
Автор ответа:
1
Решения на двух фотографиях
Приложения:


Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: nastta1534
Предмет: Алгебра,
автор: aishiteimasu
Предмет: Русский язык,
автор: Htoya11037
Предмет: История,
автор: норм18
Предмет: Физика,
автор: lyanova1