Предмет: Математика,
автор: evaava098
2^(x)+8/2^(x)-8 + 2^(x)-8/2^(x)+8 ≥ 2^(x+4)+96/4^(x)-64
Приложения:
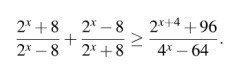
Ответы
Автор ответа:
12
2^(x)+8/2^(x)-8 + 2^(x)-8/2^(x)+8 ≥ 2^(x+4)+96/4^(x)-64
x≠3
2^x+8/2^x-8 + 2^x-8/2^x+8 ≥ 2^x*2^4+96/(2^2)^x-64
2^x+8/2^x-8 + 2^x-8/2^x+8 ≥ 2^x*2^4+96/t^2-64
t∈(-∞; -8)∪(8; +∞)∪{4}
2^x∈(-∞; -8)∪(8; +∞)∪{4}
2^x<-8
2^x>8
2^x=4
x∉0
x>3
x=2
x∈(3; +∞)∪{2}
x≠3
2^x+8/2^x-8 + 2^x-8/2^x+8 ≥ 2^x*2^4+96/(2^2)^x-64
2^x+8/2^x-8 + 2^x-8/2^x+8 ≥ 2^x*2^4+96/t^2-64
t∈(-∞; -8)∪(8; +∞)∪{4}
2^x∈(-∞; -8)∪(8; +∞)∪{4}
2^x<-8
2^x>8
2^x=4
x∉0
x>3
x=2
x∈(3; +∞)∪{2}
Похожие вопросы
Предмет: Английский язык,
автор: bes936
Предмет: Биология,
автор: soa545239
Предмет: Математика,
автор: mishaopium
Предмет: Математика,
автор: яхта2кы
Предмет: Математика,
автор: Лиза7429