Предмет: Математика,
автор: gusak007
вычислить границы:
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
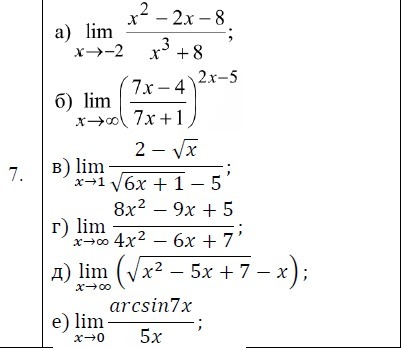
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: alishermirtursunov
Предмет: История,
автор: der91212
Предмет: Английский язык,
автор: Shumurovaisdari
Предмет: Физика,
автор: kholodovichana
Предмет: Математика,
автор: настя7872