Предмет: Алгебра,
автор: richav
1+sqrt((1+x)(sqrt(x^2-24)))=x помогите пожалуйста решить!!!
Приложения:
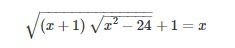
ShirokovP:
вы точно правильно написали условие?
можно расписать прям, пожалуйста!
Ответы
Автор ответа:
1
Возведем обе части уравнения в квадрат
(x + 1)* sqrt(x^2 - 24) = (x - 1)^2
Возведем обе части уравнения в квадрат
(x + 1)^2*(x^2 - 24) = (x - 1)^4
x^2(x + 1)^2 - 24(x + 1)^2 = x^4 - 4x^3 + 6x^2 - 4x + 1
x^4 + 2x^3 - 23x^2 - 48x - 24 = x^4 - 4x^3 + 6x^2 - 4x + 1
2x^3 - 23x^2 - 48x - 24 = - 4x^3 + 6x^2 - 4x + 1
6x^3 - 29x^2 - 44x - 25 = 0
Дальше см скриншот
===========================
(x + 1)* sqrt(x^2 - 24) = (x - 1)^2
Возведем обе части уравнения в квадрат
(x + 1)^2*(x^2 - 24) = (x - 1)^4
x^2(x + 1)^2 - 24(x + 1)^2 = x^4 - 4x^3 + 6x^2 - 4x + 1
x^4 + 2x^3 - 23x^2 - 48x - 24 = x^4 - 4x^3 + 6x^2 - 4x + 1
2x^3 - 23x^2 - 48x - 24 = - 4x^3 + 6x^2 - 4x + 1
6x^3 - 29x^2 - 44x - 25 = 0
Дальше см скриншот
===========================
Приложения:

Решал по методу Виета-Кардано.
спасибо!
в ответ запиши только первый корень
Похожие вопросы
Предмет: Другие предметы,
автор: darinafox007
Предмет: Биология,
автор: anastasia66624
Предмет: Алгебра,
автор: vladimirar18
Предмет: Математика,
автор: goharbadalyan
Предмет: Алгебра,
автор: skaid