Question

Пожалуйста, срочно
Найти площадь фигуры, ограниченной параболой y=(x+1)², прямой y=1-x и осью Ох
С рисунком, даю 14б!

Answer 1

Ответ:

S = 5/6

Объяснение:

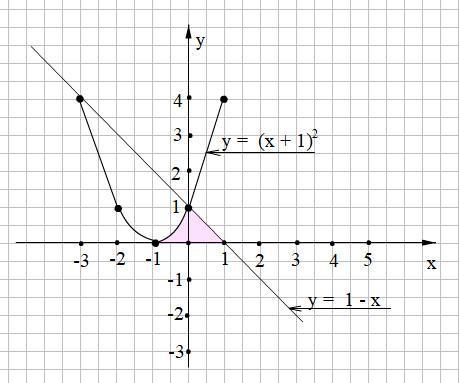
Смотри прикреплённый рисунок.

Строим графики функций у = (х + 1)²   и   у = 1 - х

Находим область, ограниченную графиками этих функций и прямой у = 0. Видим, что эта область состоит из двух частей. 1-я часть расположена под кривой  у = (х + 1)² при х ∈ (-1; 0) и 2-я часть - под прямой у = 1 - х при х ∈ (0; 1).

$S = \int\limits^0_{-1} {(x + 1)^{2}} \ dx + \int\limits^1_0 {(1-x)} \ dx =\\ \\ = \int\limits^0_{-1} {(x + 1)^{2}} \ d(x+1) - \int\limits^1_0 {(x-1)} \ d(x-1) =$

$= \frac{(x+1)^{3}}{3} \Big |_{-1}^{0}- \frac{x-1}{2}\Big |_{0}^{1} = \frac{1}{3}- 0 -0+\frac{1}{2}=\frac{5}{6}$