Предмет: Алгебра,
автор: Aktan11
помогите пожалуйста срочно дам 50 баллов
Приложения:
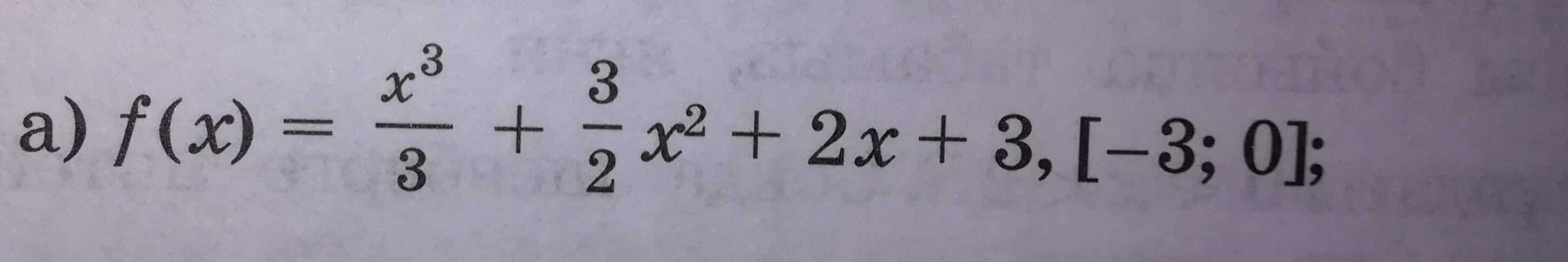
Ответы
Автор ответа:
1
Найдём производную:
Найдём нули производной :
x² + 3x + 2 = 0
D = 3² - 4 * 1 * 2 = 9 - 8 = 1
Найдём значения функции в критических точках и на концах отрезка и сравним их .
Наибольшее значение на отрезке [- 3 ; 0] равно 3 , а наименьшее 1,5 .
Похожие вопросы
Предмет: Английский язык,
автор: kotik29162
Предмет: Математика,
автор: DIMADANEVICH
Предмет: Геометрия,
автор: lerikabersimenko
Предмет: Алгебра,
автор: ILoveOwls
Предмет: Математика,
автор: KseniaP3