Предмет: Математика,
автор: reyzi77
Нужно решить два неопределенных и два определенных интеграла.
Приложения:
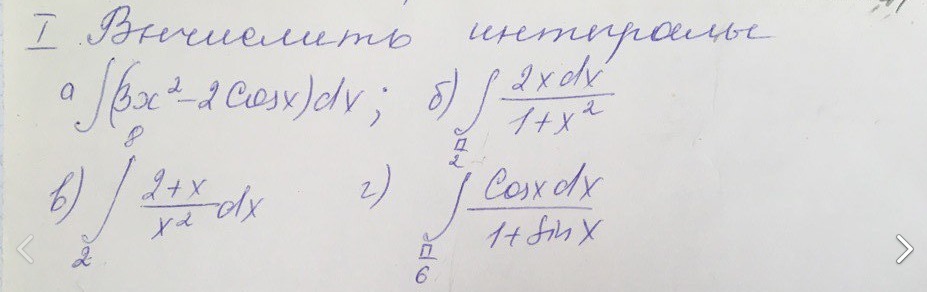
Ответы
Автор ответа:
1
Приложения:
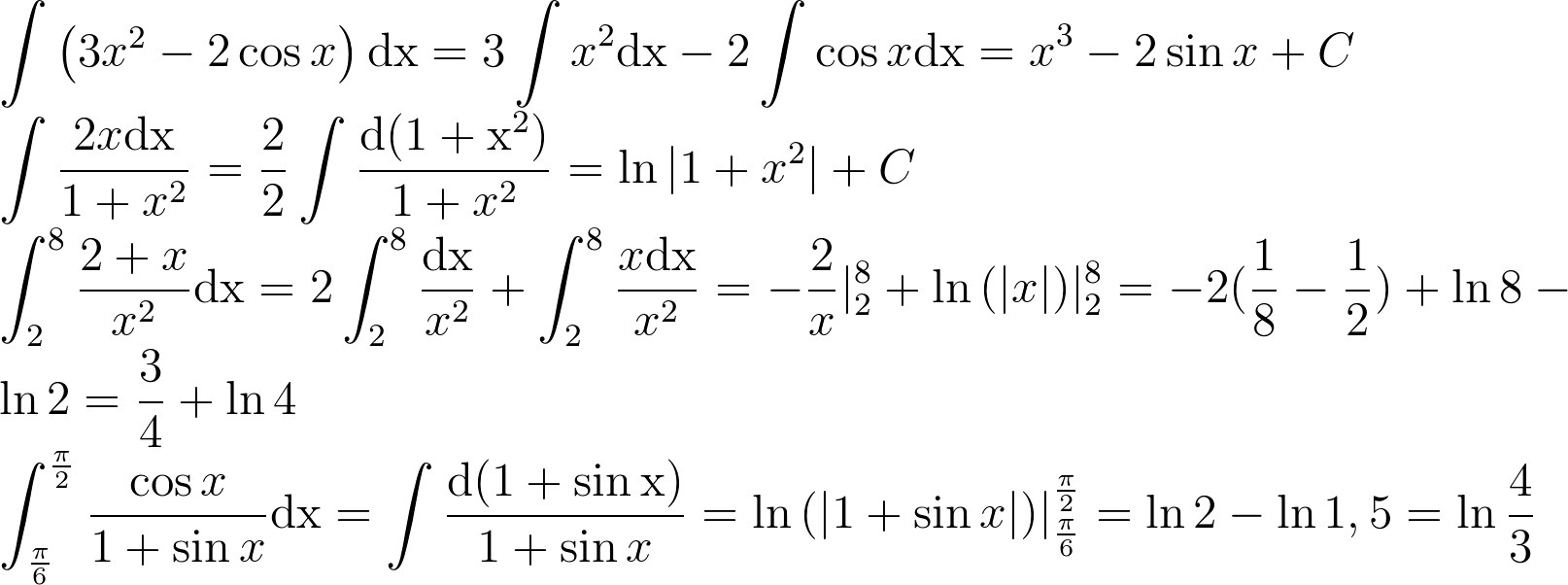
Похожие вопросы
Предмет: Литература,
автор: ekaterinavatchenko
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: roman912938
Предмет: Алгебра,
автор: mamedovanolik