Question

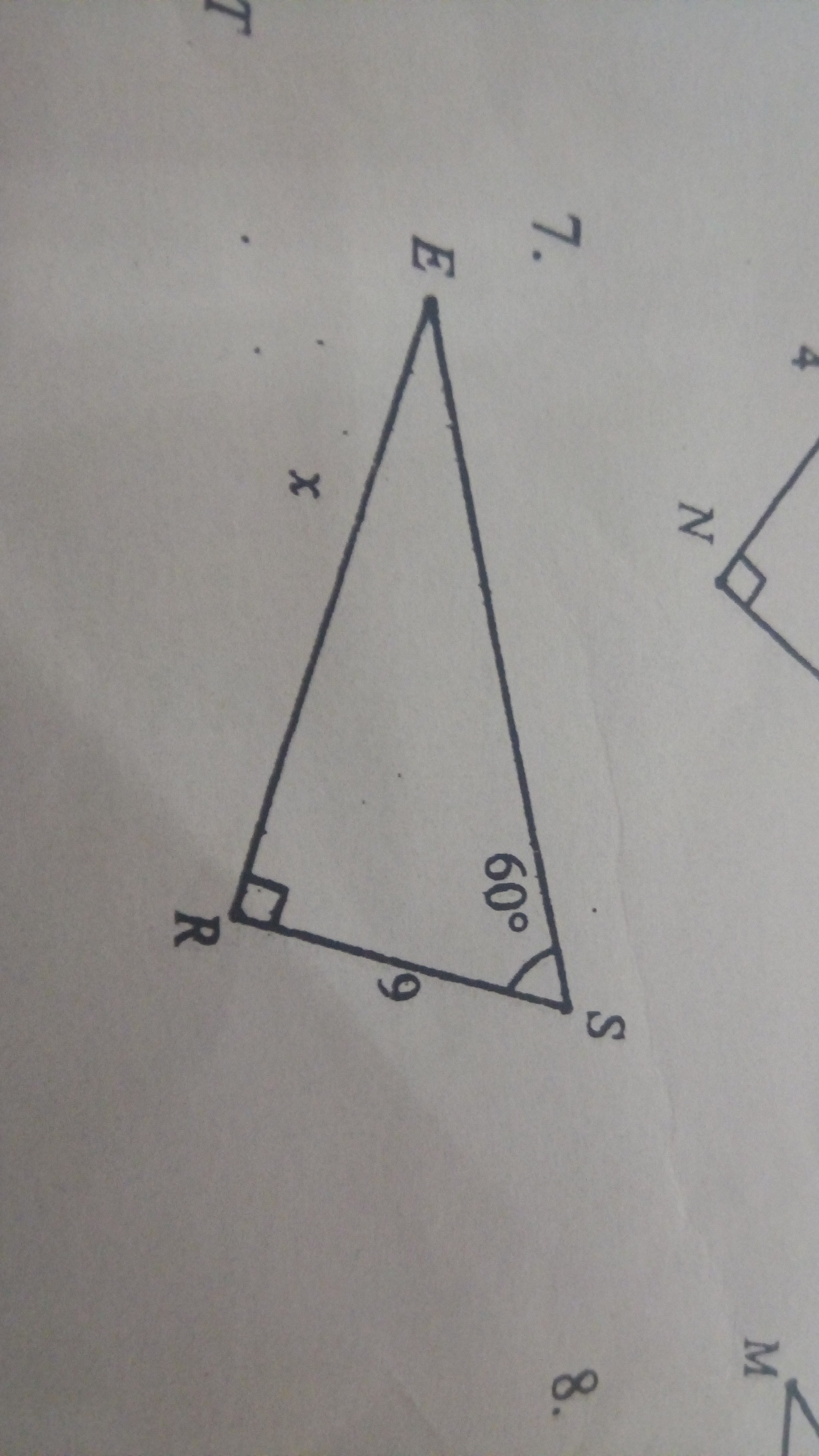
Треугольник ERS, SR=9, угол S=60°, Найти: ER

Answer 1

Ответ:

$9\sqrt{3}$

Объяснение:

1 способ.

$\angle R = 90^{\circ}$, по рисунку, значит $\triangle ERS$ - прямоугольный.

По теореме о сумме острых углов в прямоугольном треугольнике $\angle E = \angle R - \angle S = 90^{\circ} - 60^{\circ} = 30^{\circ}$.

По теореме об угле в 30° в прямоугольном треугольнике $ES = SR * 2 = 9 * 2 = 18$

По теореме Пифагора:

$ER^{2} = ES^{2} - SR^{2} = 18^{2} - 9^{2} = 324 - 81 = 243$

$ER = \sqrt{243} = 9\sqrt{3}$

2 способ.

$\angle R = 90^{\circ}$, по рисунку, значит $\triangle ERS$ - прямоугольный.

• Если угол прямоугольного треугольника равен 60°, то противолежащий катет равен произведению меньшего катета на √3.

$\Rightarrow ER = SR * \sqrt{3} = 9* \sqrt{3} = 9\sqrt{3}$