Предмет: Геометрия,
автор: matskevichales
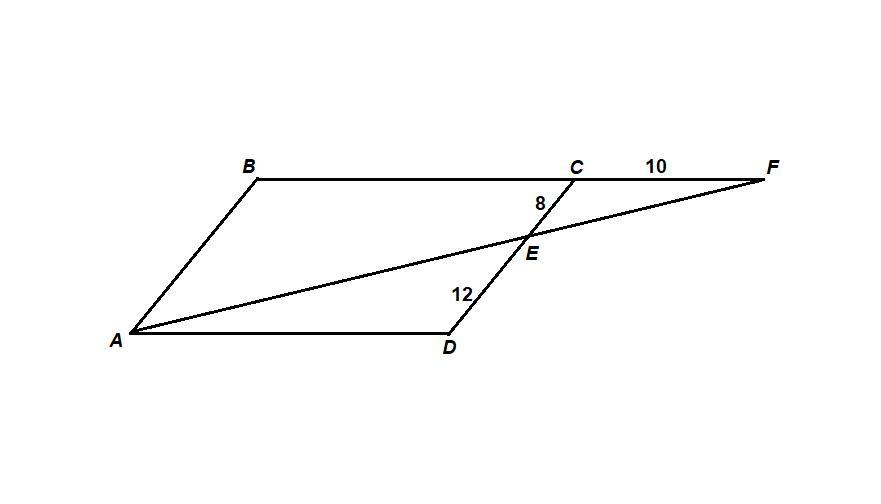
На стороне CD параллелограмма ABCD отмечена точка E. Прямые AE и BC пересекаются в точке F. Найти BC если известно, что EC = 8 CF = 10 DE=12.
Ответы
Автор ответа:
2
Ответ:
15
Объяснение:
∠EDA = ∠FCE как накрест лежащие при пересечении параллельных прямых AD и CF секущей CD,
∠AED = ∠FEC как вертикальные, значит
ΔAED ~ ΔFEC по двум углам.
ВС = AD = 15 как противоположные стороны параллелограмма.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: murtuzalievavika
Предмет: Английский язык,
автор: sviridovamaria92
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: makc5744