Question

Сколько корней имеет уравнение 99sin x=x?

Answer 1

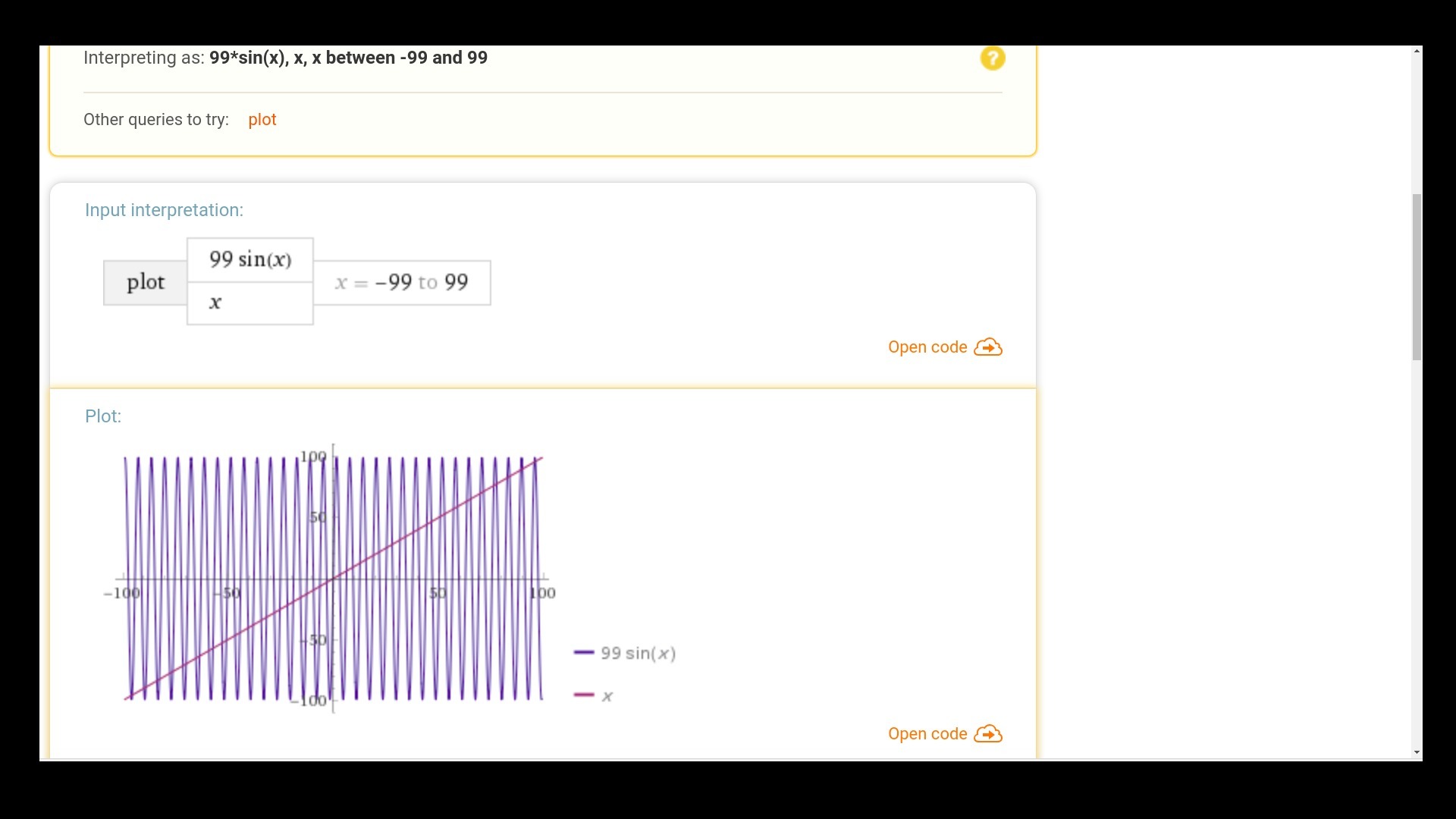
решение графическое! точки пересечения графиков функций левой и правой частей уравнения соответствуют решениям уравнения!

график функции $f(x)=99*sin(x)$ это растянутый вдоль оси OY в 99 раз график функции $sin(x)$, нужно отметить, что функциия $f(x)$ - нечётная функция и проходит через точку $(0;0)$

$-99 \leq f(x) \leq 99$

график функции $g(x)=x$ - обычная себе прямая линия, с наклоном $45^0$ к оси ОХ, также проходящая через точку $(0;0)$

из вышеизложенного, прямая линия функции $g(x)=x$ будет пересекать "гребни" функции $f(x)$, начиная с значения -99 и пока её значение не привысит 99, а это случиться, на промежутке $x\in[-99;99]$

на промежутке $x\in[0;99]$ прямая линия пересекает только "положительные гребни" синусоиды при чем на один период есть только один положительный гребень, и каждый гребень эта прямая линия будет пересикать в двух точках. Сколькои таких гребней, столько и периодов на промежутке $x\in[0;99]$:
$\frac{99}{2\pi}\approx15.8$
на таком количестве периодов находиться 16 "положительных гребней", т.е. есть 32 точки пересечения

аналогично для промежутка  $x\in[-99;0]$ (точки пересечения будут уже с "отрицательными гребнями" синусоиды) - 32 точки пересечения

но на промежутке $x\in[-99;99]$ будет на одну точку пересечения меньше, потому как точка пересечения $(0;0)$ учитывалась в обоих промежутках

Ответ: $32*2-1=63$