Question

Из точки к прямой проведены две наклонные, длины которых равны 11 см и 16 см. Найдите проекции данных наклонных, если одна из проекций на 9см меньше другой.
Пожалуйста с рисунком, на котором все расписанно

Answer 1

Ответ:     3 см,  12 см.

Объяснение:

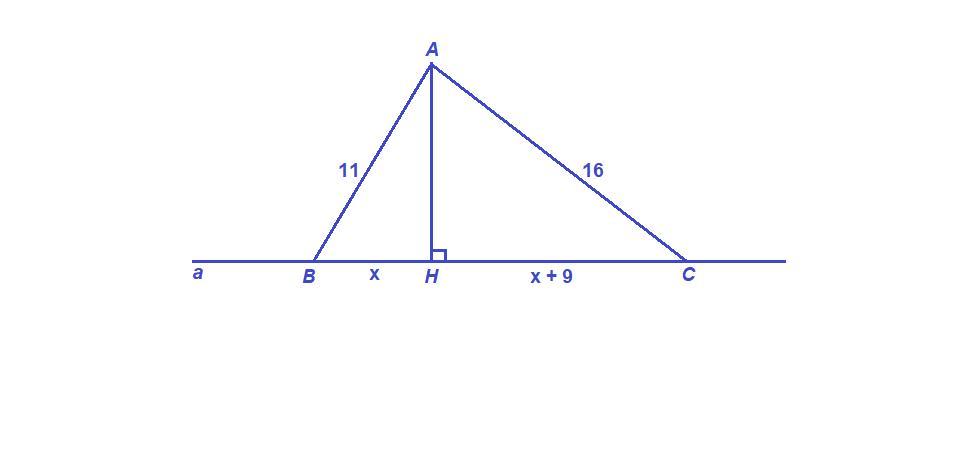
АВ = 11 см   и   АС = 16 см  - наклонные к прямой а,

АН - перпендикуляр к прямой а, тогда

ВН и СН - проекции соответствующих наклонных.

Большей наклонной соответствует большая проекция.

Пусть ВН = х см, тогда СН = (х + 9) см.

Из прямоугольного треугольника АВН по теореме Пифагора выразим АН:

АН² = АВ² - ВН²

АН² = 11² - x² = 121 - x²

И выразим АН по теореме Пифагора из прямоугольного треугольника АСН:

AH² = AC² - CH²

AH² = 16² - (x + 9)² = 256 - (x² + 18x + 81) =

= 256 - x² - 18x - 81 = 175 - x²- 18х

Приравняем правые части получившихся равенств:

121 - x² = 175 - x²- 18х

18x = 54

x = 3

ВН = 3 см

СН = 3 + 9 = 12 см