Предмет: Геометрия,
автор: Olik004
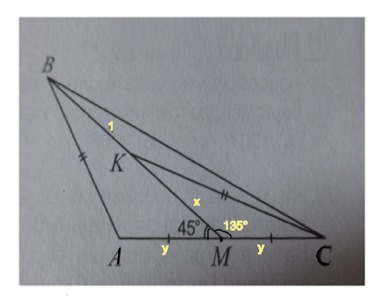
В треугольнике АВС проведена медиана ВМ. Известно,что угол АМВ=45°. На отрезке ВМ выбрана точка К такая,что АВ = КС. Оказалось,что ВК = 1. Найдите АС
А)1,75
Б)√3
В)1,5
Г)√2
Д)1
Ответы
Автор ответа:
0
Примем АМ=МС=y
Примем КМ=х, тогда ВМ=х+1
По т.косинусов
АВ²=ВМ²+АМ²-2•ВМ•АМ•cos(BMA)
KC²=KM²+MC²-2•KM•MC•cos(KMC)
Угол ВМС смежный углу ВМА и равен 180°-45°=135°
cos 45°=√2/2
cos135°= -√2/2
Подставим в уравнения принятые значения отрезков:
АВ²=(х+1)²+у²-2•[(х+1)•у√2]/2
АВ²=х²+2х+1+у² -ху√2-y√2⇒
AB²=х²+у²+2х+1-ху√2-y√2 (1)
КС²=х²+у²-2ху•(-√2/2)
KC²=x²+y²+xy√2 (2)
По условию АВ=КС => уравнение 1=уравнению 2
Вычтя из уравнения (2) уравнение (1), получим
0=ху√2-2х-1+ху√2+y√2 =>
(2xy√2+y√2) - (2х+1)=0
y√2(2x+1)-(2x+1)=0
Сократим на (2х+1)
y√2-1=0
y√2=1 =>
y=1/√2
AC=2y=2/√2=√2
Приложения:
Похожие вопросы
Предмет: Химия,
автор: stadnikovvital
Предмет: Физика,
автор: mparfentjev
Предмет: Українська мова,
автор: sffitio
Предмет: Литература,
автор: Legenda988
Предмет: Математика,
автор: ПаркаМан