Question

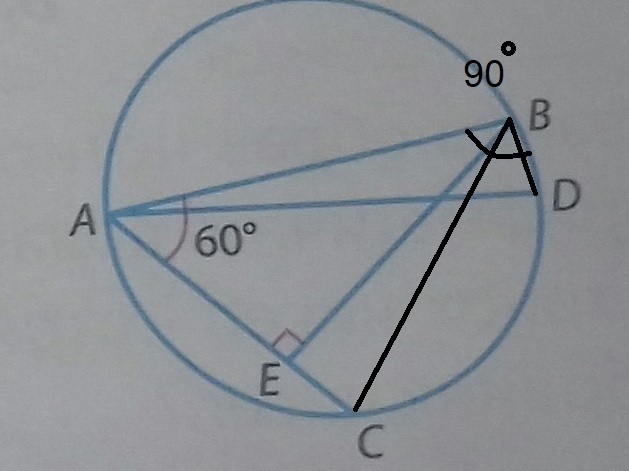
В окружности с диаметром AD проведены хорды AB и AC так , что угол BAC равен 60 градусам. Известно , что AB =24 , AC= 15 . Найдите длину отрезка BD.

Answer 1

Проведем хорду  ВС.  

ВЕ=24*sin 60°= 12√3

Уточнения: угол АВЕ = 30° (180° -90° -60°) ; sin 30° = 0,5, следовательно АЕ=0,5 *АВ= 12 , откуда ЕС = АС – АЕ = 15 – 12 =3 . Из прямоугольного треугольника ВЕС, находим, по теореме Пифагора, гипотенузу ВС:

BC=√(144*3+9)= √441 =21

По  формуле 

для  хорды   ВС=2R*sin 60°  находим диаметр круга:

2R=D= 21/ sin 60° =21*2/√3= 14√3

Треугольник ABD  прямоугольный,  так  как,   вписанный

угол, опирающийся на диаметр окружности -  прямой.

Хорда  BD= √196*3-576=√12= 2√3