Question

Диагональное сечение правильной четырехугольной пирамиды является прямоугольным треугольником, площадь которого равна 9 см2. Найдите объем пирамиды. Ответ запишите числом без наименования.

Answer 1

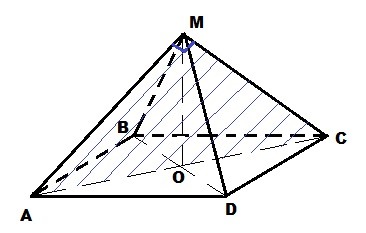
MABCD - правильная четырёхугольная пирамида  ⇒ 
ABCD - квадрат   и     MA = MB = MC = MD
Диагональное сечение  MAC - прямоугольный треугольник ⇒
∠AMC = 90°.  SΔ = 9 см²
ΔMAC прямоугольный равнобедренный  ⇒
MO = OC = OA  ⇒  MO = 1/2 AC
$S_{MAC} = \frac{AC*MO}{2} =9$
AC*MO = 18;    AC* 1/2 AC = 18
AC² = 36   ⇒    AC = 6 см;    MO = 6/2 = 3 см

Основание пирамиды - квадрат, площадь квадрата через равные диагонали
$S_o = S_{ABCD}= \frac{AC*BD}{2} = \frac{6*6}{2} =18$
Объём пирамиды
$V = \frac{1}{3} MO*S_o = \frac{1}{3} *3*18 = 18$ см³

Ответ: объём пирамиды равен 18 см³