Предмет: Математика,
автор: khrushch8
Помогите пожалуйста решить неравенства,мне нужно найти корни хотя бы буду признателен
Уравнение в фото
Приложения:
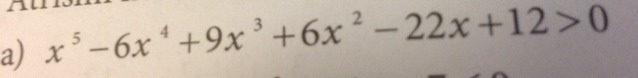
Ответы
Автор ответа:
0
Корни сначала подбираются из чисел, являющихся далителями свободного члена,
то есть числа 12.
При х=1 вычисляем левую часть неравенства,получим 0.Значит,1 - корень многочлена.Делим многочлен на (х-1), получим

Теперь с помощью подбора ищем корень многочлена во второй скобке.Это будет х=2.

Тогда исходный многочлен раскладывается на следующие множители и неравенство примет вид

то есть числа 12.
При х=1 вычисляем левую часть неравенства,получим 0.Значит,1 - корень многочлена.Делим многочлен на (х-1), получим
Теперь с помощью подбора ищем корень многочлена во второй скобке.Это будет х=2.
Тогда исходный многочлен раскладывается на следующие множители и неравенство примет вид
Похожие вопросы
Предмет: Английский язык,
автор: zukovakarina497
Предмет: Английский язык,
автор: gusejnovkerim333
Предмет: Алгебра,
автор: apchemerenko1
Предмет: Математика,
автор: пятёркаа
Предмет: Алгебра,
автор: Masheeld