Предмет: Математика,
автор: andreipantelee
Найти площадь фигуры, ограниченной графиками функций
Приложения:
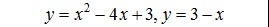
Ответы
Автор ответа:
0
1) y = x² - 4x + 3 = (x - 2)² - 1
График функции - квадратичная парабола, ветви направлены вверх. Вершина параболы в точке (2; -1)
Пересечение с осями
x = 0; y = 3
y = 0; (x-2)²-1=0; (x-2)² = 1;
x - 2 = 1 или x - 2 = -1
x = 3; x = 1
2) y = 3 - x
График - прямая линия
Точки пересечения с осями
x = 0; y = 3
y = 0; x = 3
3) точки пересечения графиков
x² - 4x + 3 = 3 - x
x² - 3x = 0
x (x - 3) = 0
x₁ = 0; x₂ = 3
y₁ = 3; y₂ = 0
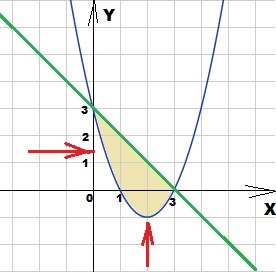
4) область интегрирования
по оси ОХ x∈[0; 3]
по оси OY от параболы y = x² - 4x + 3 до прямой y = 3 - x
5)
Вычисление интеграла прилагается
График функции - квадратичная парабола, ветви направлены вверх. Вершина параболы в точке (2; -1)
Пересечение с осями
x = 0; y = 3
y = 0; (x-2)²-1=0; (x-2)² = 1;
x - 2 = 1 или x - 2 = -1
x = 3; x = 1
2) y = 3 - x
График - прямая линия
Точки пересечения с осями
x = 0; y = 3
y = 0; x = 3
3) точки пересечения графиков
x² - 4x + 3 = 3 - x
x² - 3x = 0
x (x - 3) = 0
x₁ = 0; x₂ = 3
y₁ = 3; y₂ = 0
4) область интегрирования
по оси ОХ x∈[0; 3]
по оси OY от параболы y = x² - 4x + 3 до прямой y = 3 - x
5)
Вычисление интеграла прилагается
Приложения:
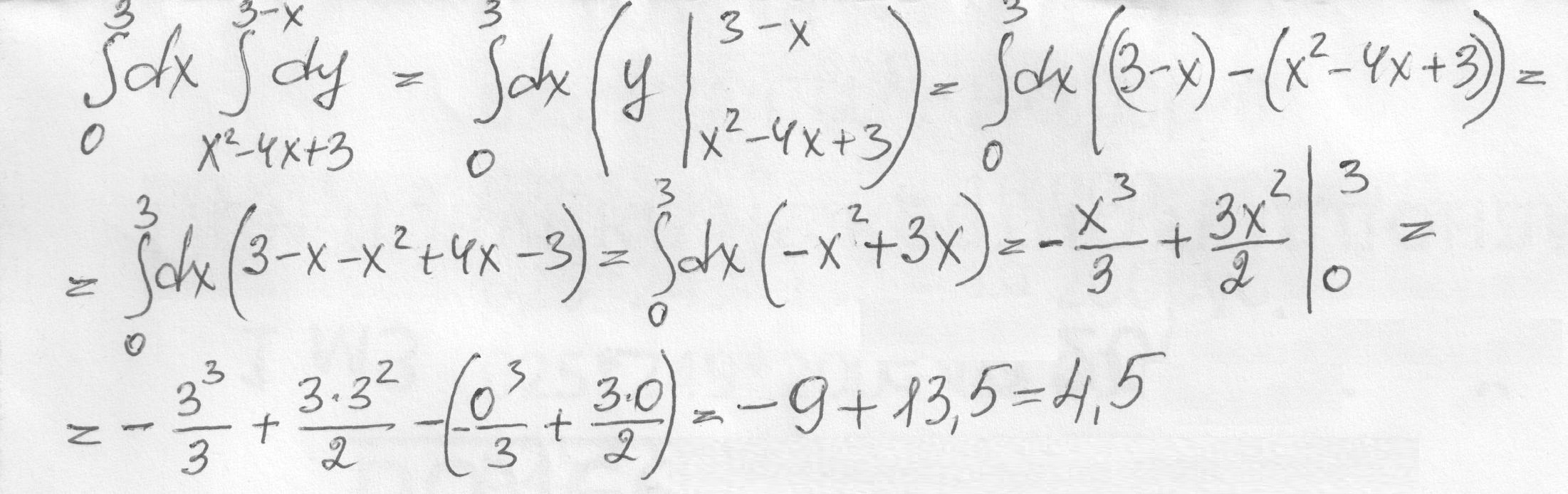
Похожие вопросы
Предмет: Математика,
автор: pvpnara
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: bekbolatovsamil9
Предмет: Математика,
автор: tun9j3aDJblov