Предмет: Математика,
автор: Nixeys4
Не смог решить. Помогите пожалуйста.
Приложения:
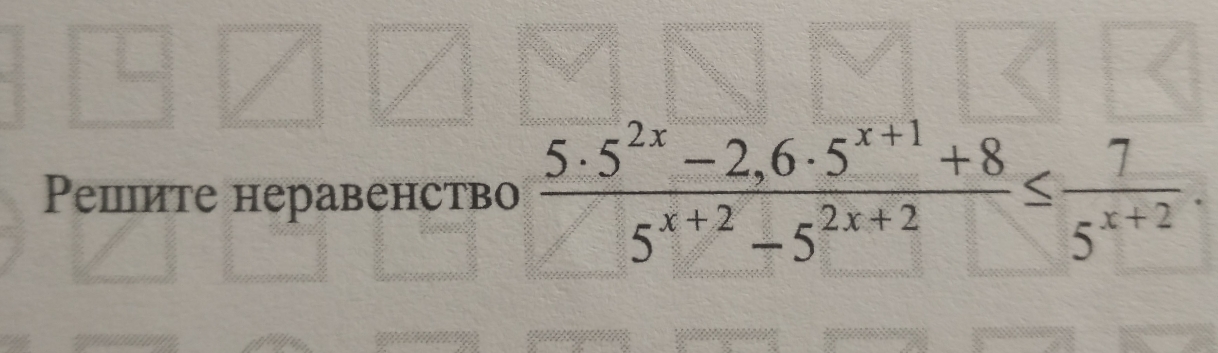
Ответы
Автор ответа:
0
одз: 5ˣ⁺²-5²ˣ⁺²≠0
25×5ˣ-25×5²ˣ≠0
25×5ˣ(1-5ˣ)≠0
1-5ˣ≠0 5ˣ≠5⁰ x≠0
(5×5²ˣ-2,6×5×5ˣ+8)/(25×5ˣ-25×5²ˣ)≤7/25×5ˣ
(5×5²ˣ-13×5ˣ+8)/25(5ˣ-5²ˣ)≤7/25×5ˣ
(5×5²ˣ-15×5ˣ+8)/(5ˣ-5²ˣ)≤7/5ˣ
5ˣ=t
(5t²-13t+8)/(t-t²)≤7/t
5t²-13t+8=0
D=169-160=9 t₁=13-3/10=1 t₂=13+3/10=1,6
5(t-1)(t-1,6)/t(1-t)≤7/t
-5(t-1,6)/t≤7/t
-5(t-1,6)≤7
t-1,6≥-1,4
t≥0,2
t≥1/5
5ˣ≥5⁻¹
x≥-1 учитывая одз х∈[-1;0)∪(0;+∞)
25×5ˣ-25×5²ˣ≠0
25×5ˣ(1-5ˣ)≠0
1-5ˣ≠0 5ˣ≠5⁰ x≠0
(5×5²ˣ-2,6×5×5ˣ+8)/(25×5ˣ-25×5²ˣ)≤7/25×5ˣ
(5×5²ˣ-13×5ˣ+8)/25(5ˣ-5²ˣ)≤7/25×5ˣ
(5×5²ˣ-15×5ˣ+8)/(5ˣ-5²ˣ)≤7/5ˣ
5ˣ=t
(5t²-13t+8)/(t-t²)≤7/t
5t²-13t+8=0
D=169-160=9 t₁=13-3/10=1 t₂=13+3/10=1,6
5(t-1)(t-1,6)/t(1-t)≤7/t
-5(t-1,6)/t≤7/t
-5(t-1,6)≤7
t-1,6≥-1,4
t≥0,2
t≥1/5
5ˣ≥5⁻¹
x≥-1 учитывая одз х∈[-1;0)∪(0;+∞)
Похожие вопросы
Предмет: Математика,
автор: serdalindanial
Предмет: Алгебра,
автор: novelia65
Предмет: Математика,
автор: loxpinox
Предмет: Алгебра,
автор: slaHelenaGkamalyad
Предмет: Математика,
автор: N7ADOr9yineriber