Предмет: Геометрия,
автор: AquAlexa
Дано:
AA1 - перпендикуляр к плоскости Альфа, АВ и АС - наклонные
Найти: х
Приложения:
Ответы
Автор ответа:
8
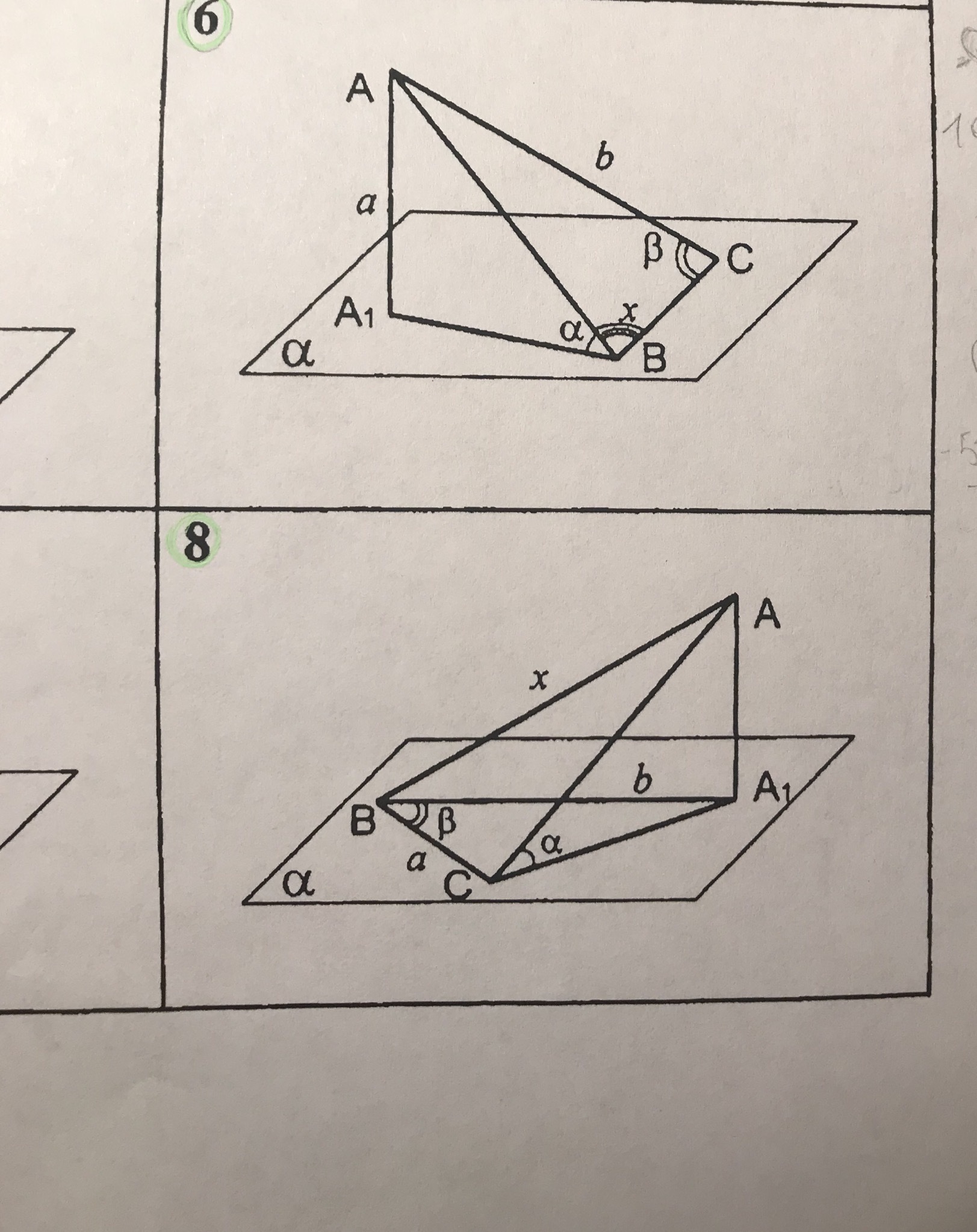
6. AA1 - перпендикуляр к плоскости Альфа ⇒
AA₁ ⊥ A₁B ⇒
ΔAA₁B - прямоугольный, ∠AA₁B = 90° ⇒

ΔABC : теорема синусов

8. ΔCBA₁ : Теорема косинусов
СA₁² = a² + b² - 2ab*cosβ
AA₁ - перпендикуляр к плоскости Альфа ⇒ AA₁⊥CA₁ ⇒
ΔCA₁A - прямоугольный, ∠CA₁A=90° ⇒
AA₁ = CA₁*tgα
AA₁ - перпендикуляр к плоскости Альфа ⇒ AA₁⊥BA₁ ⇒
ΔBA₁A - прямоугольный, ∠BA₁A =90° ⇒ по теореме Пифагора
X² = b² + AA₁² = b² + (CA₁*tgα)² =
= b² + CA₁²*tg²α = b² + (a² + b² - 2ab*cosβ)tg²α

AA₁ ⊥ A₁B ⇒
ΔAA₁B - прямоугольный, ∠AA₁B = 90° ⇒
ΔABC : теорема синусов
8. ΔCBA₁ : Теорема косинусов
СA₁² = a² + b² - 2ab*cosβ
AA₁ - перпендикуляр к плоскости Альфа ⇒ AA₁⊥CA₁ ⇒
ΔCA₁A - прямоугольный, ∠CA₁A=90° ⇒
AA₁ = CA₁*tgα
AA₁ - перпендикуляр к плоскости Альфа ⇒ AA₁⊥BA₁ ⇒
ΔBA₁A - прямоугольный, ∠BA₁A =90° ⇒ по теореме Пифагора
X² = b² + AA₁² = b² + (CA₁*tgα)² =
= b² + CA₁²*tg²α = b² + (a² + b² - 2ab*cosβ)tg²α
AquAlexa:
Спасибо большое!
Похожие вопросы
Предмет: Физика,
автор: larisaluchaya
Предмет: Русский язык,
автор: polyakovvladimir1952
Предмет: Английский язык,
автор: aidanaadoni
Предмет: Математика,
автор: tatzhigunova20
Предмет: Алгебра,
автор: hfgfffggg