Question

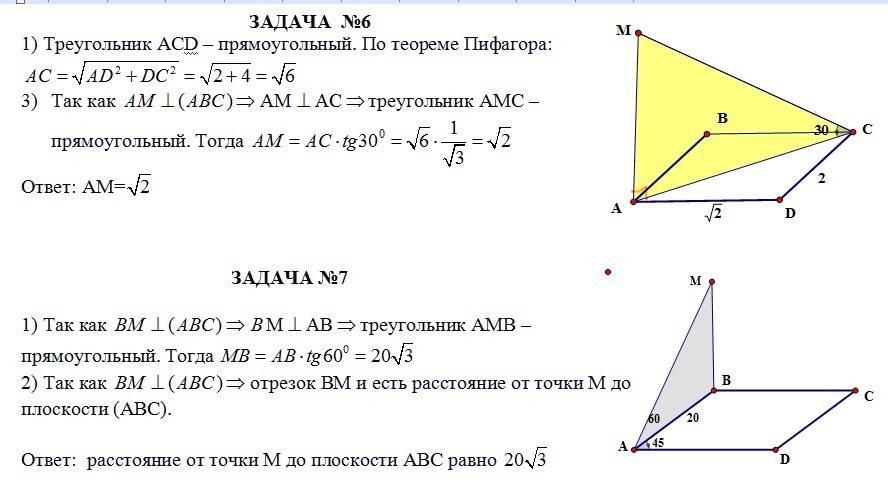
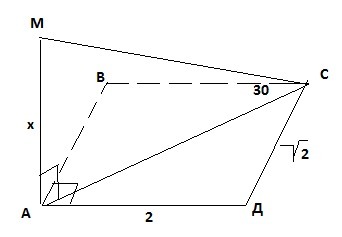
6. Отрезок АМ является перпендикуляром к плоскости прямоугольника АВСД. Угол между прямой МС и этой плоскостью равен 30°, АД = √(2), СД = 2. Найдите АМ.
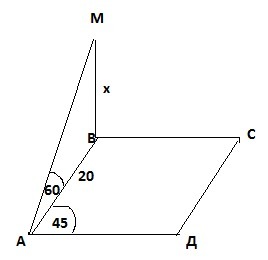
7. В параллелограмме АВСД АВ = 20 см, ВАД = 45°, ВМ - перпендикуляр к плоскости АВС. Угол между прямой МА и плоскостью АВС равен 60°. Найдите расстояние от точки М до плоскости АВС.

Answer 1

Решение смотри ниже.

Answer 2

6.  По теореме Пифагора: АС=√(АД²+ДС²)=√(2+4)=√6.
По теореме синусов:
АС/sinМ=АМ/sinС⇒  AM=AC*sin30/sin60=√6*2/2*√3=√3*√2/√3=√2
7. В ΔАМВ АВ=1/2АМ как катет в прямоугольном Δлежащий против угла в 30°, значит АМ=2АВ=2*20=40см.. 
По т. Пифагора МВ=√(АМ²-АВ²)=√(1600-400)=√1200=20√3..
К решению прикреплены 2 рисунка.