Предмет: Математика,
автор: aslanrskaliev
Найти общие и частные решения линейных дифференциальных уравнений первого порядка (у=uv)
Приложения:
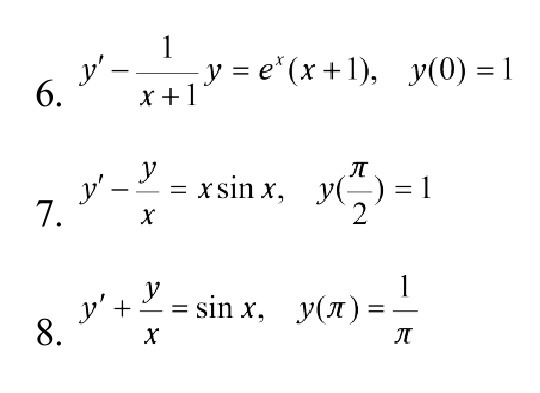
Ответы
Автор ответа:
0
6)

7)

8)


7)
8)
Автор ответа:
0
С другим оформлением решение...
Приложения:


Похожие вопросы
Предмет: Геометрия,
автор: didenkopolina44
Предмет: Русский язык,
автор: 4n42njsgm6
Предмет: История,
автор: bajtasovaaazan
Предмет: Математика,
автор: olgaf28081