Предмет: Математика,
автор: JIjwiejf
Исследовать функцию и построить график
y=-x^4+4x+3
Ответы
Автор ответа:
4
1) Функция определена на всей числовой прямой х∈R
2) Проверим четность

Так как и
и 
то функция не является четно и нечетной. Функция общего вида.
3) Точки пересечения с осью Оу: х = 0

т.е. точка А(0; 3)
4) Найдем производную

5) Найдем точке экстремума y' = 0

Получилась одна критическая точка
6) Найдем значение производной слева и справа от 1

до х=1 функция возрастает

после х=1 функция убывает
Производная меняет знак с "+" на "-" - значит х=1 точка максимума
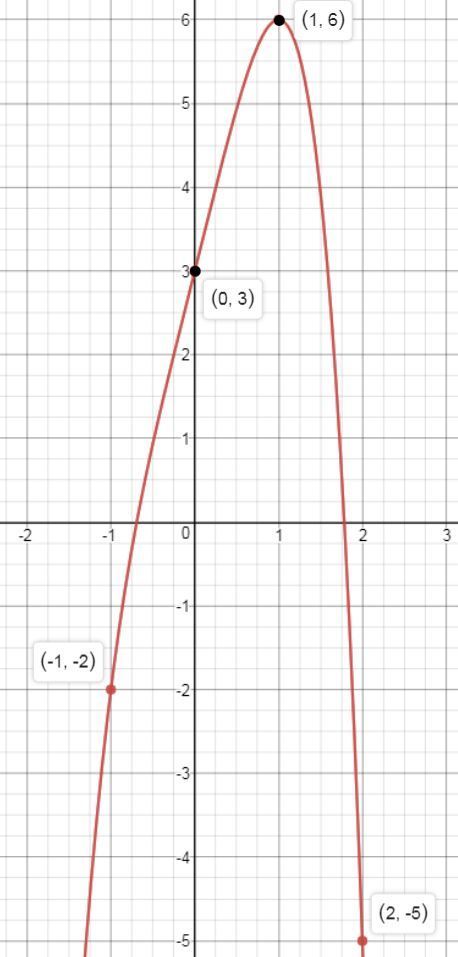
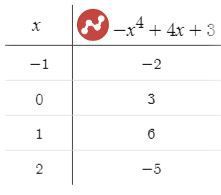
7) Построим график функции. Данные для построение и сам график, представлены ниже
2) Проверим четность
Так как
то функция не является четно и нечетной. Функция общего вида.
3) Точки пересечения с осью Оу: х = 0
т.е. точка А(0; 3)
4) Найдем производную
5) Найдем точке экстремума y' = 0
Получилась одна критическая точка
6) Найдем значение производной слева и справа от 1
до х=1 функция возрастает
после х=1 функция убывает
Производная меняет знак с "+" на "-" - значит х=1 точка максимума
7) Построим график функции. Данные для построение и сам график, представлены ниже
Приложения:
Похожие вопросы
Предмет: Математика,
автор: sulekaksenia9
Предмет: Литература,
автор: sofasekret1
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Ratinho
Предмет: Математика,
автор: Аноним