Предмет: Алгебра,
автор: Palata6EEE
Показательные уравнения.
Приложения:
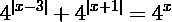
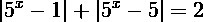
Palata6EEE:
Решение даже одного из них будет полезным ~
Ответы
Автор ответа:
1
Рассмотрим 2 случая
1)x≤0
тогда
так как |x-3|≥0 и |x+1|≥0, то
поскольку
то уравнение при x≤0 корней не имеет
2) x>0 тогда
|x-3|≥0 |x+1|=x+1 ⇒
корней нет
ОТВЕТ : КОРНЕЙ НЕТ
Похожие вопросы
Предмет: ОБЖ,
автор: ztsalko777
Предмет: Химия,
автор: musienkodiana07
Предмет: Информатика,
автор: doforeoeooe
Предмет: Математика,
автор: Аноним