Question

помогите с арифметической прогрессией))))

Answer 1

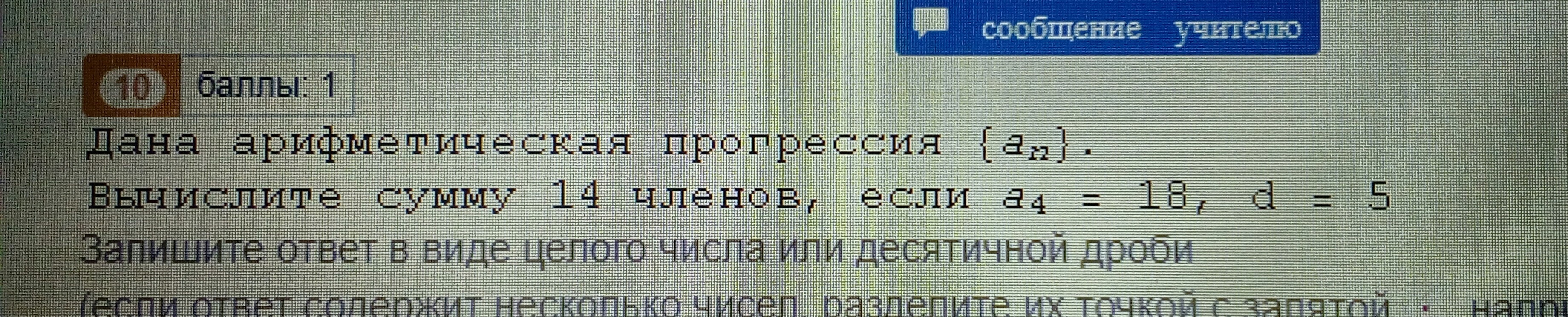
Сумма прогрессии вычисляется по формуле S(n) = ((a(1) + a(n))*n)/2
Для 14 членов она будет выглядеть так: S(14) = ((a(1) + a(14))*14)/2
Надо найти a(14).
a(n) = a(1) + d*(n-1)
Получается, что надо найти еще и a(1).
У нас есть a(4). Выведем из формулы для "a(4)" a(1).
a(4) = a(1) + d*(4-1) = a(1) + d*3
a(1) = a(4) - d*3 Подставим сюда значение d и a(4).
a(1) = 18 - 5*3 = 18 - 15 = 3

Теперь найдем a(14).
a(14) = a(1) + d*(14-1) = 3 + d*13 = 3 + 5*13 = 3 + 65 = 68

Вернемся к формуле суммы членов и подставим найденные значения.
S(14) = ((3 + 68)*14)/2 = (71 * 14)/2 = 994/2 = 497

Ответ: сумма 14 членов равна 497