Question

(log по 5 (25х^2) + 48) / (log по 5 от х^2 - 49) >= -1

Answer 1

ОДЗ: x ≠ 0 (ОДЗ логарифма)
$log_{5}{x^2}-49 neq 0 \ log_{5}{x^2} neq 49 \ x^2 neq 5^{49} \ x neq pm5^{24}sqrt{5}$

$frac{log_{5}{(25x^2)}+48}{log_{5}{x^2}-49} geq -1 \ frac{2log_{5}{(|5x|)}+48}{2log_{5}{|x|}-49} geq -1 \ frac{2(log_{5}{5}+log_{5}{|x|})+48}{2log_{5}{|x|}-49} geq -1 \ frac{2(1+log_{5}{|x|})+48}{2log_{5}{|x|}-49} geq -1 \ frac{2+2log_{5}{|x|}+48}{2log_{5}{|x|}-49} geq -1 \ frac{2log_{5}{|x|}+50}{2log_{5}{|x|}-49} geq -1$
Пусть $2log_{5}{|x|}=t$
$frac{t+50}{t-49} geq -1 \ frac{t+50}{t-49} + 1 geq 0 \ frac{2t+1}{t-49} geq 0 \ left [ {{t leq -0.5} atop {t textgreater 49}} right. \ left [ {{2log_{5}{|x| leq -0.5}} atop {2log_{5}{|x|} textgreater 49}} right. \ left [ {{log_{5}{|x|} leq -0.25} atop {log_{5}{|x|} textgreater frac{49}{2} }} right. \ left [ {{log_{5}{|x|} leq log_{5}{5^{- frac{1}{4} }}} atop {log_{5}{|x|} textgreater log_{5}{5^{frac{49}{2}}} }} right.$
$left [ {{|x| leq frac{1}{ sqrt[4]{5} } } atop {|x| textgreater sqrt{5^{49}} }} right. \ left [ { -frac{ sqrt[4]{125} }{5}leq {x leq frac{ sqrt[4]{125} }{5} } atop { left [ {{x textless -5^{24} sqrt{5} } atop {x textgreater 5^{24} sqrt{5} }} right. }} right.$

Учитывая ОДЗ, получаем ответ:
$xin(-infty; -5^{24} sqrt{5})cup[-frac{ sqrt[4]{125} }{5}; 0)cup(0; frac{ sqrt[4]{125} }{5}]cup(5^{24}sqrt{5}; +infty)$

Answer 2

Спасибо большое)

Answer 3

log(5)(25x²)+48=log(5)25+log(5)x²+48=2+2log(5)x+48=log(5)x+50
log(5)x²-49=2log(5)x-49
----------------------------------------------
x>0
(2log(5)x+50)/(2log(5)x-49)≥-1
(2log(5)x+50)/(2log(5)x-49)+1≥0
(2log(5)x+50+2log(5)x-49)/(2log(5)x-49)≥0
(4log(5)x+1)/(2log(5)x-49)≥0
log(5)x=t
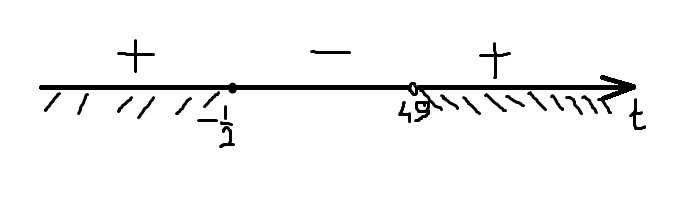
(4t+1)/(2t-49)≥0
t=-1/4  t=49/2
       +                         _                   +
-----------[-1/4]----------------(49/2)-------------
t≤-1/4⇒log(5)x≤-1/4⇒$x leq 1/ sqrt[4]{5}$
t>49/2⇒log(5)x>49/2⇒x>$5 ^{24} sqrt{5}$
Ответ ∈(0;$1/ sqrt[4]{5}$] U ($5 ^{24} sqrt{5}$;∞)