Предмет: Алгебра,
автор: annabelova2017
ребят, как здесь применить метод рационализации?
Приложения:
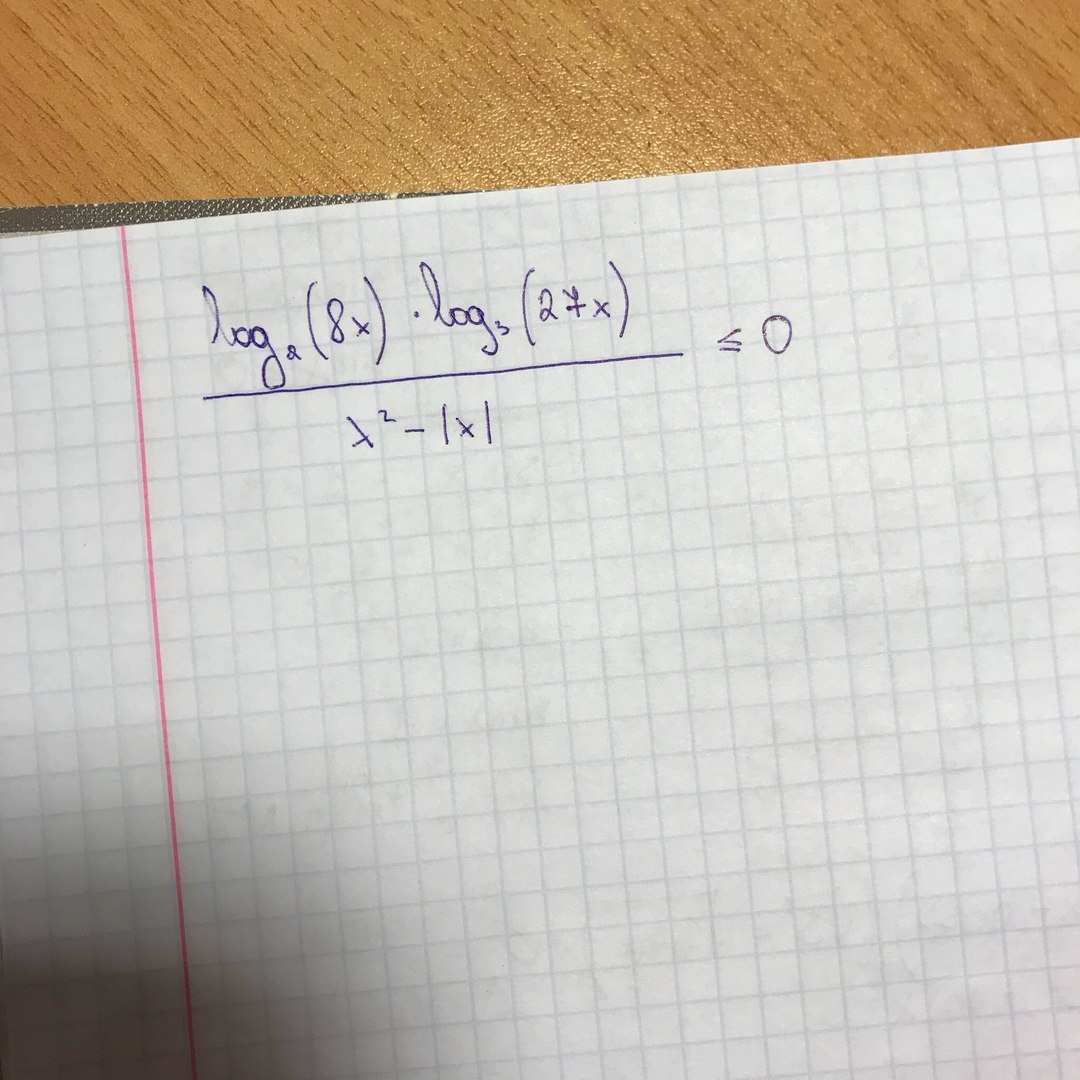
Ответы
Автор ответа:
0
Для начала отметим ОДЗ:
x > 0
Есть такой метод, как
Тогда

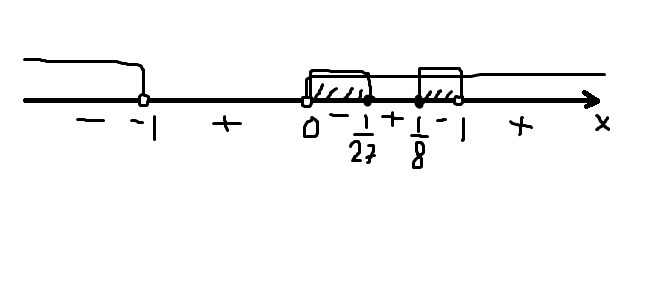
Отмечаем корни:

Учитываем ОДЗ и получаем ответ.
Ответ:![xin(0; frac{1}{27}]cup[ frac{1}{8} ;1) xin(0; frac{1}{27}]cup[ frac{1}{8} ;1)](https://tex.z-dn.net/?f=xin%280%3B++frac%7B1%7D%7B27%7D%5Dcup%5B+frac%7B1%7D%7B8%7D+%3B1%29)
x > 0
Есть такой метод, как
Тогда
Отмечаем корни:
Учитываем ОДЗ и получаем ответ.
Ответ:
Приложения:
Автор ответа:
0
т.е. можно применить этот метод только к числителю ?
Автор ответа:
0
Нет, можно и к знаменателю.
Похожие вопросы
Предмет: Алгебра,
автор: jvkree
Предмет: Русский язык,
автор: simenovavika
Предмет: Алгебра,
автор: mobiland05092021
Предмет: Геометрия,
автор: 1Neyda4nik1
Предмет: История,
автор: bell2010