Предмет: Алгебра,
автор: Аффтапелод
Найдите производную функции:
1) f(x)=(2x+3)/(3x+5);
2) f(x)=(x+3)/(x-1).
Ответы
Автор ответа:
0
1) f(x)=(2x+3)/(3x+5);
f`(x=[(2x+3)`*(3x+5)-(3x+5)`(2x+3)]/(3x+5)²=[2(3x+5)-3(2x+3)]/(3x+5)²=
=(6x+10-6x-9)/(3x+5)²=1/(3x+5)²
2) f(x)=(x+3)/(x-1).
f`(x)=[1*(x-1)-1*(x+3)]/(x-1)²=(x-1-x-3)/(x-1)²=-4/(x-1)²
f`(x=[(2x+3)`*(3x+5)-(3x+5)`(2x+3)]/(3x+5)²=[2(3x+5)-3(2x+3)]/(3x+5)²=
=(6x+10-6x-9)/(3x+5)²=1/(3x+5)²
2) f(x)=(x+3)/(x-1).
f`(x)=[1*(x-1)-1*(x+3)]/(x-1)²=(x-1-x-3)/(x-1)²=-4/(x-1)²
Автор ответа:
0
Огромное Вам спасибо. =)
Автор ответа:
0
Решение на фото
Удачи;)
Удачи;)
Приложения:
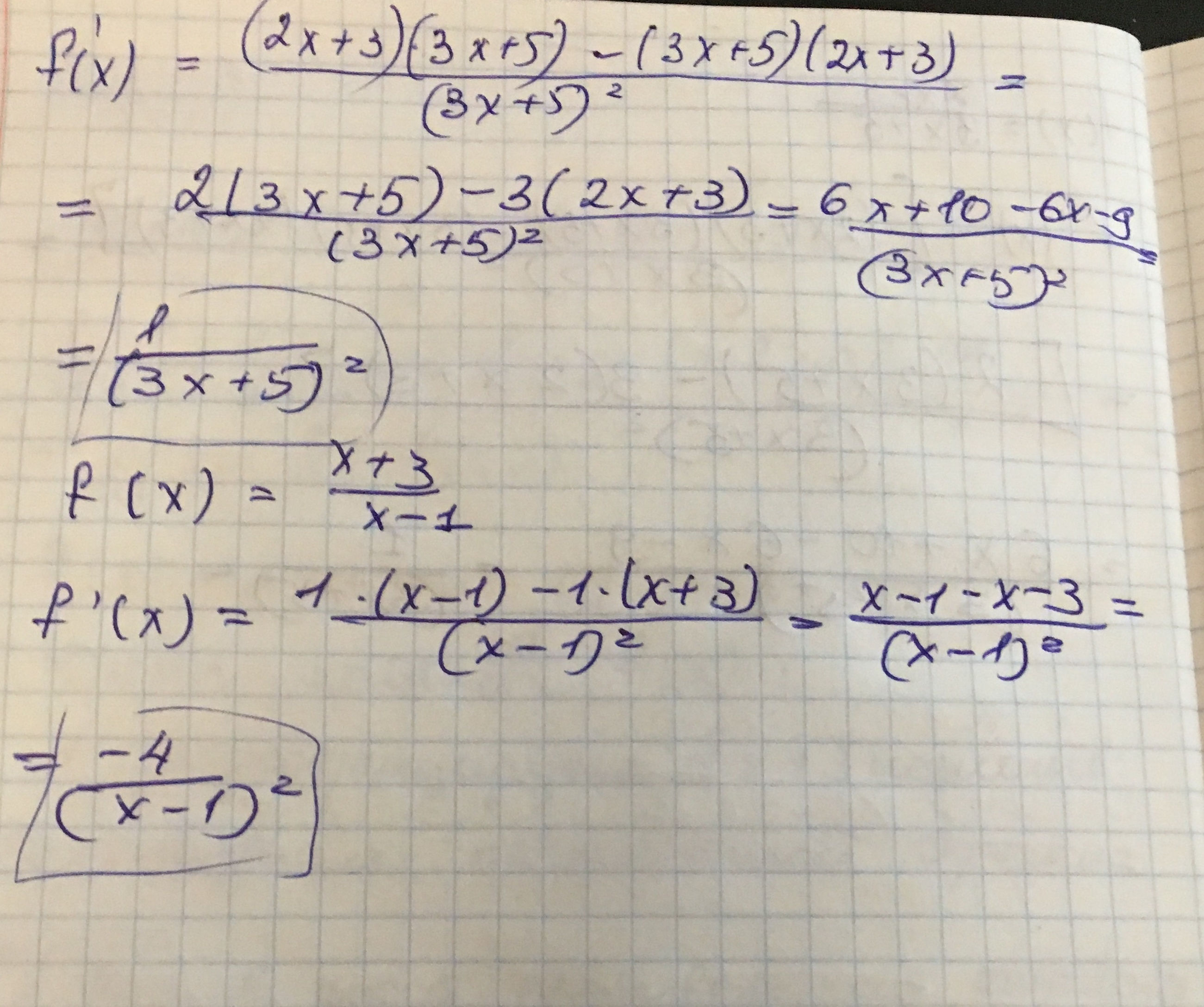
Автор ответа:
0
Спасибо Вам. ;)
Похожие вопросы
Предмет: Геометрия,
автор: lgzk
Предмет: Английский язык,
автор: inaraalieva66
Предмет: Английский язык,
автор: stasjcue3
Предмет: Химия,
автор: artem3076
Предмет: География,
автор: Vilioh